第十章作业8 带电粒子在电场中的运动

第1题 (多选题) 难度 - 基础题：

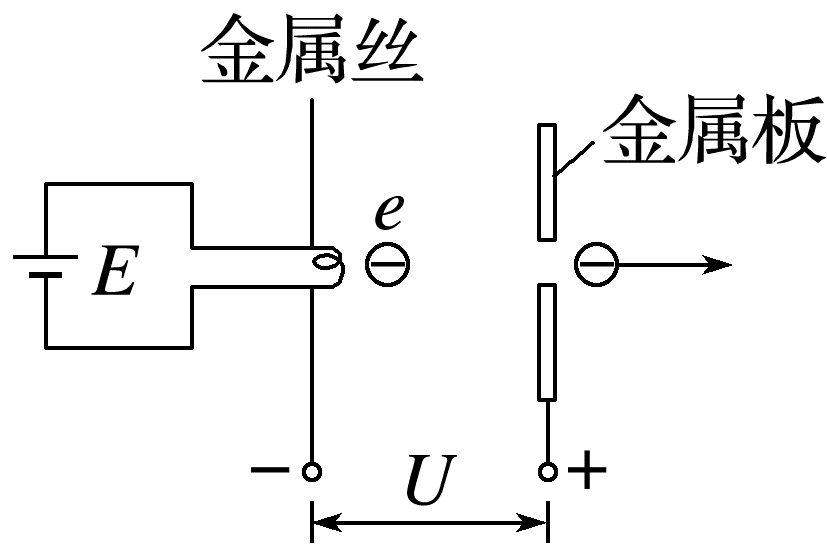
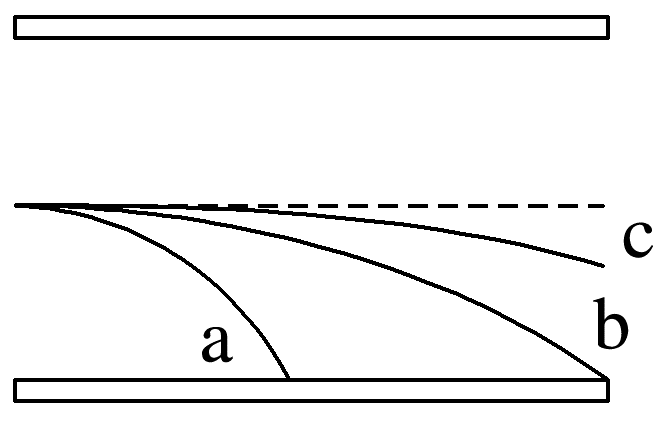
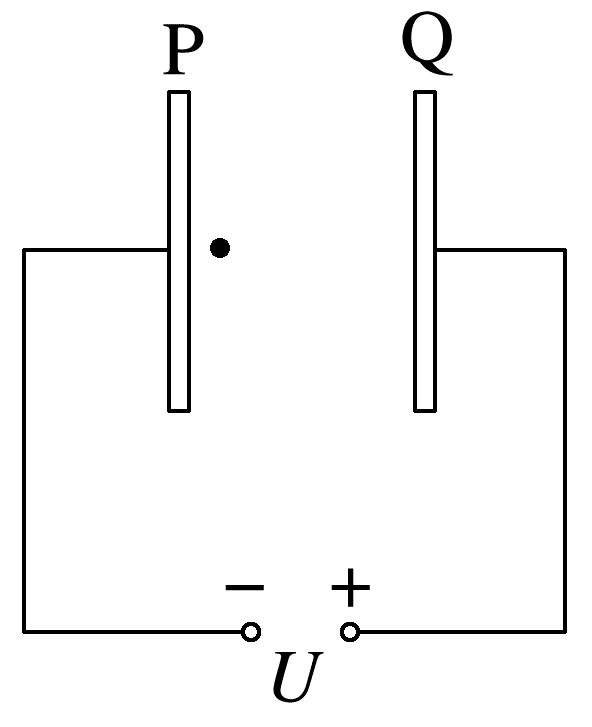
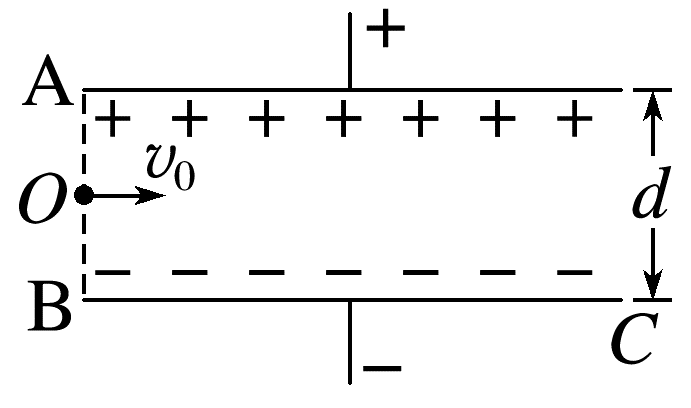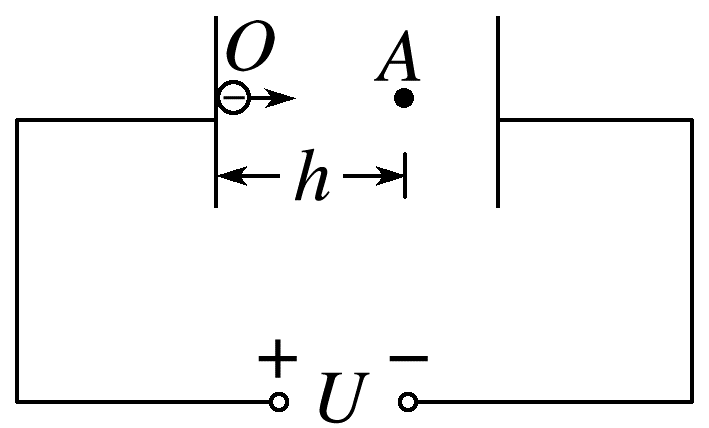(多选)(2024·南阳市高二期末)如图所示，P、Q两极板间电压为U，在P板附近有一电子(电荷量为－e、质量为m)仅在静电力作用下由静止开始向Q板运动，则(　　)

A: 电子到Q板时速率为 $\sqrt{\frac{e U}{2 m}}$
B: 两极板间距离越大，电子到达Q板时速率越大
C: 两极板间距离越小，电子在两极板间运动的加速度越大
D: 电子到达Q板时速率与两极板间距离无关

解析:

根据动能定理有eU＝ $\frac{1}{2}$ mv²解得v＝ $\sqrt{\frac{2 e U}{m}}$ ，可知电子到达Q板时速率与两极板间距离无关，故A、B错误，D正确；

根据牛顿第二定律有a＝ $\frac{q E}{m} ＝ \frac{q U}{m d}$

可知两极板间距离越小，电子在两极板间运动的加速度越大，故C正确。

第2题 (填空题) 难度 - 基础题：

(来自教材改编)某些肿瘤可以用“质子疗法”进行治疗。在这种疗法中，质子先被加速到具有较高的能量，然后被引向轰击肿瘤，杀死细胞，如图所示。若质子的加速长度为4.0 m，要使质子由静止被加速到1.0×10⁷ m/s，加速匀强电场的电场强度大小为　　　　 N/C。(质子质量为1.67×10^－²⁷ kg，电荷量为1.6×10^－¹⁹ C，结果保留两位有效数字)

答案:

1.3×10⁵

解析:

由动能定理得Eq·d＝ $\frac{1}{2}$ mv²，所以E＝ $\frac{m v^{2}}{2 q d} ＝ \frac{1.67 \times 10^{- 27} \times (1.0 \times 10^{7})^{2}}{2 \times 1.6 \times 10^{- 19} \times 4.0}$ N/C≈1.3×10⁵ N/C。

第3题 (计算题) - 简答题难度 - 基础题：

(来自鲁科教材)炽热的金属丝可发射电子。如图所示，在金属丝和金属板之间加上U＝2 500 V的电压，发射出的电子在真空中加速后，从金属板的小孔穿出。设电子刚刚离开金属丝时的速度为0，取电子电荷量的大小e＝1.6×10^－¹⁹ C，质量m＝9.1×10^－³¹ kg，求电子穿出小孔时的动能和速度。

答案:

4×10¹⁶ J　3×10⁷ m/s

解析:

在加速电场中，由动能定理得E_k＝eU＝1.6×10^－¹⁹ C×2 500 V＝4×10^－¹⁶ J。

电子穿出小孔时的动能E_k＝ $\frac{1}{2}$ mv²，即v＝ $\sqrt{\frac{2 E_{k}}{m}}$ ，得电子穿出小孔时的速度v≈3×10⁷ m/s。

第4题 (单选题) 难度 - 基础题：

(2024·重庆市巴渝学校高二期中)如图所示，带电平行金属板水平放置，电荷量相同的三个带电粒子a、b、c从两极板正中央以相同的初速度垂直电场线方向射入匀强电场(不计粒子的重力)，则它们在两板间运动的过程中(　　)

A: a、b、c粒子在板间运动时间t_a＝t_b<t_c
B: a、b、c粒子在板间运动时间t_a<t_b＝t_c
C: a、b、c粒子在板间运动时间t_a＝t_b＝t_c
D: a、b、c粒子在板间运动时间t_a＝t_b>t_c

解析:

三个带电粒子a、b、c从两极板正中央以相同的初速度垂直电场线方向射入匀强电场，则水平方向均做匀速直线运动，因x_a<x_b＝x_c，根据x＝v₀t可知t_a<t_b＝t_c。故选B。

第5题 (单选题) 难度 - 基础题：

(2024·西安市高二期中)平行板间距为d，长度为l，加上电压后，可在A、B之间的空间中(设为真空)产生电场(设为匀强电场)。在距A、B两平行板等距离的O点处，有一电荷量为＋q、质量为m的粒子以初速度v₀沿水平方向(与A、B板平行)射入，不计重力，要使此粒子恰好能从下极板边缘C处射出，则A、B间的电压应为(　　)

A: $\frac{q v_{0}}{d l}$
B: $\frac{m {v_{0}}^{2} l^{2}}{q d^{2}}$
C: $\frac{l m v_{0}}{q d}$
D: $\frac{m {v_{0}}^{2} d^{2}}{q l^{2}}$

解析:

带电粒子只受静电力作用，在平行板间做类平抛运动。设粒子由O点到C处的运动时间为t，则有l＝v₀t，

设A、B间的电压为U，则平行板间的匀强电场的电场强度为E＝ $\frac{U}{d}$ ，

粒子所受静电力为F＝qE＝ $\frac{q U}{d}$

根据牛顿第二定律得粒子沿电场方向的加速度为a＝ $\frac{F}{m} ＝ \frac{q U}{m d}$ ，粒子在沿电场方向做匀加速直线运动，位移为 $\frac{1}{2}$ d，由匀变速直线运动的规律得 $\frac{d}{2} ＝ \frac{1}{2}$ at²

联立解得U＝ $\frac{m {v_{0}}^{2} d^{2}}{q l^{2}}$ ，故选D。

第6题 (单选题) 难度 - 中档题：

如图所示，带电荷量之比为q_A∶q_B＝1∶3的带电粒子A、B，先后以相同的速度从同一点水平射入平行板电容器中，不计重力，带电粒子偏转后打在同一极板上，水平飞行距离之比为x_A∶x_B＝2∶1，则带电粒子的质量之比m_A∶m_B以及在电场中飞行的时间之比t_A∶t_B分别为(　　)

A: 1∶1，2∶3
B: 2∶1，3∶2
C: 1∶1，3∶4
D: 4∶3，2∶1

解析:

粒子在水平方向上做匀速直线运动，则x＝v₀t，由于初速度相同，且x_A∶x_B＝2∶1，所以t_A∶t_B＝2∶1，竖直方向上粒子做匀加速直线运动，y＝ $\frac{1}{2}$ at²，且y_A＝y_B，故a_A∶a_B＝ ${t_{B}}^{2}$ ∶ ${t_{A}}^{2}$ ＝1∶4，由ma＝qE得m＝ $\frac{q E}{a}$ ， $\frac{m_{A}}{m_{B}} ＝ \frac{q_{A}}{q_{B}}$ · $\frac{a_{B}}{a_{A}} ＝ \frac{1}{3}$ × $\frac{4}{1} ＝ \frac{4}{3}$ 。综上所述，选项D正确。

第7题 (填空题) 难度 - 中档题：

(来自教材改编)如图，两平行金属板相距为d，电势差为U，一个电子从O点沿垂直于极板的方向射出，最远到达A点，然后返回。已知O、A两点相距为h，电子质量为m，电子的电荷量为e，则此电子在O点射出时的速度大小为　　　　　　　　(用所给字母表示)。

答案:

$\sqrt{\frac{2 U e h}{d m}}$

解析:

两金属板间的电场强度为E＝ $\frac{U}{d}$

由动能定理得－Ee·h＝0－ $\frac{1}{2}$ mv²

两式联立，得v＝ $\sqrt{\frac{2 U e h}{d m}}$ 。

第8题 (计算题) - 简答题难度 - 中档题：

(来自鲁科教材)如图所示，真空中有一电子以速度v沿着与电场强度垂直的方向自O点进入匀强电场。以O为坐标原点建立平面直角坐标系，x轴垂直于电场方向，y轴平行于电场方向，在x轴上取OA＝AB＝BC，分别自A、B、C点作与y轴平行的线，跟电子的径迹交于M、N、P三点，求：

(1)电子经M、N、P三点时，沿y轴的分速度之比；

(2)电子从O点开始每经过相等时间的动能增量之比。

答案:

(1)1∶2∶3　(2)1∶3∶5

解析:

(1)电子所受静电力方向竖直向下，水平方向做匀速直线运动，即水平分速度始终不变，如果水平位移相等，则经历的时间相等，故电子从O点到M、N、P三点所用时间之比t₁∶t₂∶t₃＝1∶2∶3，电子竖直方向做匀加速直线运动，因为v_yM＝at₁，v_yN＝at₂，v_yP＝at₃，所以沿y轴的分速度之比为1∶2∶3。

(2)竖直方向位移为y＝ $\frac{1}{2}$ at²，y与t²成正比，三段运动时间相同，沿y轴方向的位移之比y_AM∶y_BN∶y_CP＝1∶4∶9，

所以竖直方向位移之比y_AM∶y_MN∶y_NP＝1∶3∶5，

则由动能定理得eEy_AM＝ΔE_k1，eEy_MN＝ΔE_k2，eEy_NP＝ΔE_k3，可求得电子从O点开始每经过相等时间的动能增量之比为1∶3∶5。

第9题 (计算题) - 简答题难度 - 中档题：

(来自教材)先后让一束电子和一束氢核通过同一对平行板形成的偏转电场，进入时速度方向与电场方向垂直。在下列两种情况下，分别求出电子偏转角的正切与氢核偏转角的正切之比。

(1)电子与氢核的初速度相同。

(2)电子与氢核的初动能相同。

答案:

见解析

解析:

设偏转电压为U，带电粒子电荷量为q，质量为m，进入偏转电场的速度为v₀，偏转电场两极板间的距离为d，极板长度为L，对带电粒子有：初动能E_k＝ $\frac{1}{2}$ m ${v_{0}}^{2}$ ，在偏转电场中的加速度a＝ $\frac{q U}{m d}$ ，在偏转电场中运动的时间t＝ $\frac{L}{v_{0}}$ ，离开偏转电场时沿静电力方向的速度v_⊥＝at＝ $\frac{q U}{m d}$ · $\frac{L}{v_{0}}$ ，离开偏转电场时的偏转角度θ的正切值tan θ＝ $\frac{v_{⊥}}{v_{0}} ＝ \frac{q U L}{m d {v_{0}}^{2}}$ 。

(1)电子与氢核的初速度相同，有 $\frac{t a n θ_{e}}{t a n θ_{H}} ＝ \frac{m_{H}}{m_{e}}$ 。

(2)电子与氢核的初动能相同，有 $\frac{t a n θ_{e}}{t a n θ_{H}}$ ＝1。

第10题 (计算题) - 简答题难度 - 中档题：

(来自鲁科教材)如图所示，一质量为m、电荷量为q的带正电粒子在匀强电场中运动，A、B为其运动轨迹上的两点。已知该粒子在A点的速度大小为v₀，方向与电场方向的夹角为60°；它运动到B点时速度方向与电场方向的夹角为30°。不计重力，求A、B两点间的电势差。

答案:

$\frac{m {v_{0}}^{2}}{q}$

解析:

设带电粒子在B点的速度大小为v_B。粒子在垂直于电场方向上的速度分量不变，即

v_Bsin 30°＝v₀sin 60°①

由此得v_B＝ $\sqrt{3}$ v₀②

设A、B两点间的电势差为U_AB，由动能定理有

qU_AB＝ $\frac{1}{2}$ m( ${v_{B}}^{2} － {v_{0}}^{2}$ )③

联立②③式得U_AB＝ $\frac{m {v_{0}}^{2}}{q}$ 。

第十章 作业8 带电粒子在电场中的运动

第十章作业8 带电粒子在电场中的运动