第一章作业6 空间中点、直线和平面的向量表示

第1题 (单选题) 难度 - 基础题：

若P(0，1，1)，Q(2，3，5)在直线l上，则直线l的一个方向向量的坐标为

A: (1，1，2)
B: (1，2，1)
C: (1，2，2)
D: (2，2，2)

解析:

由P(0，1，1)，Q(2，3，5)，得 $\vec{P Q}$ =(2，2，4)=2(1，1，2)，所以直线l的一个方向向量的坐标为(1，1，2).

第2题 (单选题) 难度 - 基础题：

已知直线l的一个方向向量为(-5，3，2)，另一个方向向量为(x，y，8)，则x+y等于

A: 8
B: -8
C: 6
D: -6

解析:

∵同一条直线的方向向量平行，

∴ $\frac{x}{- 5}$ = $\frac{y}{3}$ = $\frac{8}{2} ，$

∴x=-20，y=12，x+y=-8.

第3题 (单选题) 难度 - 基础题：

设A是空间一定点，n为空间内任一非零向量，满足条件 $\vec{A M}$ ·n=0的点M构成的是

A: 圆
B: 平面
C: 直线
D: 线段

解析:

由题意知 $\vec{A M}$ ⊥n，所以点M构成的是经过点A，且以n为法向量的平面.

第4题 (多选题) 难度 - 基础题：

(多选)在如图所示的空间直角坐标系中，ABCD-A₁B₁C₁D₁是棱长为1的正方体，下列结论中正确的是

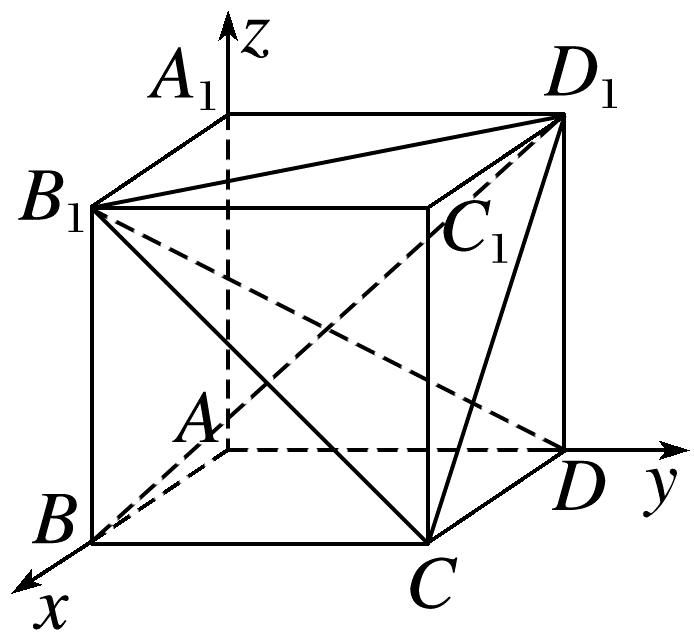
A: 直线BD₁的一个方向向量为(-2，2，2)
B: 直线BD₁的一个方向向量为(2，2，2)
C: 平面B₁CD₁的一个法向量为(1，1，1)
D: 平面B₁CD的一个法向量为(1，-1，-1)

解析:

由题意，B(1，0，0)，B₁(1，0，1)，C(1，1，0)，D(0，1，0)，D₁(0，1，1).

对于A，B项，可知 $\vec{B D_{1}}$ =(-1，1，1)，

所以向量(-2，2，2)为直线BD₁的一个方向向量，故A正确，B不正确；

对于C项，设平面B₁CD₁的法向量为n=(x，y，z)，则 $\{\begin{array}{l} n \cdot \vec{C B_{1}} = 0, \\ n \cdot \vec{C D_{1}} = 0 . \end{array}$

又 $\vec{C B_{1}}$ =(0，-1，1) $， \vec{C D_{1}}$ =(-1，0，1)，

所以 $\{\begin{array}{l} - y + z = 0, \\ - x + z = 0 . \end{array}$

令x=1，可得n=(1，1，1)，故C正确；

对于D项，设平面B₁CD的法向量为m=(a，b，c)，则 $\{\begin{array}{l} m \cdot \vec{C B_{1}} = 0, \\ m \cdot \vec{C D} = 0 . \end{array}$

又 $\vec{C B_{1}}$ =(0，-1，1) $， \vec{C D}$ =(-1，0，0)，

所以 $\{\begin{array}{l} - b + c = 0, \\ - a = 0 . \end{array}$

令b=1，得m=(0，1，1)，故D不正确.

第5题 (单选题) 难度 - 基础题：

已知平面α={P|n· $\vec{P_{0} P}$ =0}，其中点P₀(-1，2，5)，平面α的法向量n=(1，1，1)，则下列各点在平面α内的是

A: A(1，2，3)
B: B(0，3，6)
C: C(1，1，1)
D: D(0，0，0)

解析:

对于A， $\vec{P_{0} A}$ =(2，0，-2)，则 n· $\vec{P_{0} A}$ =2×1+0×1+(-2)×1=0，则点A在平面α内，故A正确；

对于B $， \vec{P_{0} B}$ =(1，1，1)，则 n· $\vec{P_{0} B}$ =1×1+1×1+1×1=3≠0，则点B不在平面α内，故B错误；

对于C $， \vec{P_{0} C}$ =(2，-1，-4)，则 n· $\vec{P_{0} C}$ =2×1+(-1)×1+(-4)×1=-3≠0，则点C不在平面α内，故C错误；

对于D $， \vec{P_{0} D}$ =(1，-2，-5)，则 n· $\vec{P_{0} D}$ =1×1+(-2)×1+(-5)×1=-6≠0，则点D不在平面α内，故D错误.

第6题 (多选题) 难度 - 基础题：

(多选)已知空间中A(0，0，0)，B(2，1，0)，C(-1，2，1)三点，则下列说法正确的是

A: $\vec{A B}$ 与 $\vec{A C}$ 是共线向量
B: 与 $\vec{A B}$ 同向的单位向量是 $(\frac{2 \sqrt{5}}{5} ， \frac{\sqrt{5}}{5} ， 0)$
C: $\vec{B C}$ 在 $\vec{A B}$ 方向上的投影向量是(-2，-1，0)
D: 平面ABC的一个法向量是(1，-2，5)

解析:

$\vec{A B}$ =(2，1，0) $， \vec{A C}$ =(-1，2，1)， $\vec{B C}$ =(-3，1，1)，

若 $\vec{A B}$ 与 $\vec{A C}$ 共线，

设 $\vec{A B}$ =λ $\vec{A C} ，$ 则 $\{\begin{array}{l} 2 = - λ, \\ 1 = 2 λ, \\ 0 = λ, \end{array}$

方程无解，故 $\vec{A B}$ 与 $\vec{A C}$ 不共线，A错误；

与 $\vec{A B}$ 同向的单位向量是 $\frac{\vec{A B}}{|\vec{A B}|}$ = $\frac{(2 ， 1 ， 0)}{\sqrt{5}}$ = $(\frac{2 \sqrt{5}}{5} ， \frac{\sqrt{5}}{5} ， 0) ，$ B正确；

$\vec{B C}$ 在 $\vec{A B}$ 方向上的投影向量是 $\frac{\vec{A B} \cdot \vec{B C}}{|\vec{A B}|}$ · $\frac{\vec{A B}}{|\vec{A B}|}$ = $\frac{- 6 + 1}{\sqrt{5}}$ · $\frac{(2 ， 1 ， 0)}{\sqrt{5}}$ =(-2，-1，0)，C正确；

设平面ABC的法向量是n=(x，y，z)，

则 $\{\begin{array}{l} n \cdot \vec{A B} = 2 x + y = 0, \\ n \cdot \vec{A C} = - x + 2 y + z = 0, \end{array}$

令y=-2，则n=(1，-2，5)，D正确.

第7题 (单选题) 难度 - 基础题：

从点A(2，-1，7)沿向量a=(8，9，-12)的方向取线段长| $\vec{A B}$ |=34，则B点的坐标为

A: (18，17，-17)
B: (-14，-19，17)
C: $(6 ， \frac{7}{2} ， 1)$
D: $(- 2 ， - \frac{11}{2} ， 13)$

解析:

设B点坐标为(x，y，z)，

则 $\vec{A B}$ =λa(λ>0)，

即(x-2，y+1，z-7)=λ(8，9，-12)，

因为| $\vec{A B}$ |=34，

即 $\sqrt{64 λ^{2} + 81 λ^{2} + 144 λ^{2}}$ =34，解得λ=2，

所以x=18，y=17，z=-17.

第8题 (填空题) 难度 - 基础题：

在空间直角坐标系中，两平面α与β分别以n₁=(2，1，1)与n₂=(0，2，1)为其法向量，若α∩β=l，则直线l的一个方向向量为　　　　.(写出一个方向向量的坐标)

答案:

$(\frac{1}{2} ， 1 ， - 2)$ (答案不唯一)

解析:

设直线l的方向向量为d=(x，y，z)，

则 $\{\begin{array}{l} d ⊥ n_{1}, \\ d ⊥ n_{2}, \end{array}$ 所以 $\{\begin{array}{l} 2 x + y + z = 0, \\ 2 y + z = 0, \end{array}$

令y=1，则z=-2，x= $\frac{1}{2} ，$ 所以直线l的一个方向向量为d= $(\frac{1}{2} ， 1 ， - 2)$ .

第9题 (填空题) 难度 - 基础题：

已知A(1，0，0)，B(0，1，0)，C(0，0，1)，若点P(a，1，1)在平面ABC内，则a=　　　　.

答案:

-1

解析:

设平面ABC的法向量是n=(x，y，z)，

又 $\vec{A B}$ =(-1，1，0) $， \vec{A C}$ =(-1，0，1)，

所以 $\{\begin{array}{l} n \cdot \vec{A B} = - x + y = 0, \\ n \cdot \vec{A C} = - x + z = 0, \end{array}$ 取x=1，得n=(1，1，1)，

因为P(a，1，1)在平面ABC内 $， \vec{A P}$ =(a-1，1，1)，

则n· $\vec{A P}$ =a-1+1+1=0，解得a=-1.

第10题 (解答题) - 简答题难度 - 基础题：

已知A(2，2，2)，B(2，0，0)，C(0，2，-2).

(1)写出直线BC的一个方向向量；

(2)设平面α经过点A，且 $\vec{B C}$ 是α的法向量，M(x，y，z)是平面α内的任意一点，试写出x，y，z满足的关系式.

答案:

解　(1)∵B(2，0，0)，C(0，2，-2)，∴ $\vec{B C}$ =(-2，2，-2)，

即(-2，2，-2)为直线BC的一个方向向量.(答案不唯一)

(2)由题意得 $\vec{A M}$ =(x-2，y-2，z-2)，

∵ $\vec{B C}$ 是平面α的法向量，

则 $\vec{B C}$ · $\vec{A M}$ =0，

即(-2，2，-2)·(x-2，y-2，z-2)=0.

∴-2(x-2)+2(y-2)-2(z-2)=0.

化简得x-y+z-2=0.

第11题 (单选题) 难度 - 基础题：

在三棱锥P-ABC中，CP，CA，CB两两垂直，AC=CB=1，PC=2，如图，建立空间直角坐标系，则下列向量是平面PAB的一个法向量的是

A: $(1 ， 1 ， \frac{1}{2})$
B: (1 $， \sqrt{2} ，$ 1)
C: (1，1，1)
D: (2，-2，1)

解析:

因为P(0，0，2)，A(1，0，0)，B(0，1，0)，

所以 $\vec{P A}$ =(1，0，-2) $， \vec{A B}$ =(-1，1，0)，

设平面PAB的法向量为n=(x，y，1)，

由 $\{\begin{array}{l} n \cdot \vec{P A} = 0, \\ n \cdot \vec{A B} = 0, \end{array}$ 即 $\{\begin{array}{l} x - 2 = 0, \\ - x + y = 0, \end{array}$

解得 $\{\begin{array}{l} x = 2, \\ y = 2, \end{array}$ 所以n=(2，2，1).

又 $(1 ， 1 ， \frac{1}{2})$ = $\frac{1}{2}$ n，

因此，平面PAB的一个法向量为 $(1 ， 1 ， \frac{1}{2})$ .

第12题 (多选题) 难度 - 基础题：

(多选)已知直线l₁的方向向量a=(2，4，x)，直线l₂的方向向量b=(2，y，2)，若|a|=6，且a⊥b，则x+y的值是

A: 1
B: -1
C: 3
D: -3

解析:

因为|a|= $\sqrt{2^{2} + 4^{2} + x^{2}}$ =6，所以x=±4.

因为a⊥b，所以a·b=2×2+4y+2x=0，

即y=-1- $\frac{1}{2}$ x，所以当x=4时，y=-3；

当x=-4时，y=1.所以x+y=1或x+y=-3.

第13题 (填空题) 难度 - 基础题：

若A $(0 ， 2 ， \frac{19}{8}) ，$ B $(1 ， - 1 ， \frac{5}{8}) ，$ C $(- 2 ， 1 ， \frac{5}{8})$ 是平面α内三点，设平面α的法向量为a=(x，y，z)，则x∶y∶z=　　　　.

答案:

2∶3∶(-4)

解析:

由已知得 $， \vec{A B}$ = $(1 ， - 3 ， - \frac{7}{4}) ，$

$\vec{A C}$ = $(- 2 ， - 1 ， - \frac{7}{4}) ，$

∵a是平面α的法向量，

∴a· $\vec{A B}$ =0，a· $\vec{A C}$ =0，

即 $\{\begin{array}{l} x - 3 y - \frac{7}{4} z = 0, \\ - 2 x - y - \frac{7}{4} z = 0, \end{array}$ 解得 $\{\begin{array}{l} x = \frac{2}{3} y, \\ z = - \frac{4}{3} y, \end{array}$

∴x∶y∶z= $\frac{2}{3}$ y∶y∶ $(- \frac{4}{3} y)$ =2∶3∶(-4).

第14题 (解答题) - 简答题难度 - 基础题：

已知点P是平行四边形ABCD所在平面外一点，如果 $\vec{A B}$ =(2，-1，-4) $， \vec{A D}$ =(4，2，0) $， \vec{A P}$ =(-1，2，-1).

(1)求证： $\vec{A P}$ 是平面ABCD的法向量；

(2)求平行四边形ABCD的面积.

答案:

(1)证明　因为 $\vec{A P}$ · $\vec{A B}$ =(-1，2，-1)·(2，-1，-4)=0 $， \vec{A P}$ · $\vec{A D}$ =(-1，2，-1)·(4，2，0)=0，

所以AP⊥AB，AP⊥AD.

又AB∩AD=A，

所以AP⊥平面ABCD.

所以 $\vec{A P}$ 是平面ABCD的法向量.

(2)解　因为| $\vec{A B}$ |= $\sqrt{2^{2} + (- 1)^{2} + (- 4)^{2}}$ = $\sqrt{21} ，$

| $\vec{A D}$ |= $\sqrt{4^{2} + 2^{2} + 0^{2}}$ =2 $\sqrt{5} ，$

$\vec{A B}$ · $\vec{A D}$ =(2，-1，-4)·(4，2，0)=6，

所以cos〈 $\vec{A B} ， \vec{A D}$ 〉= $\frac{6}{\sqrt{21} \times 2 \sqrt{5}}$ = $\sqrt{\frac{3}{35}} ，$

故sin〈 $\vec{A B} ， \vec{A D}$ 〉= $\sqrt{\frac{32}{35}} ，$

S_▱_ABCD=| $\vec{A B}$ |·| $\vec{A D}$ |sin〈 $\vec{A B} ， \vec{A D}$ 〉=8 $\sqrt{6}$ .

第15题 (单选题) 难度 - 基础题：

在长方体ABCD-A₁B₁C₁D₁中，AB=3，BC=4，CC₁=2，M在AB上.以D为原点，DA，DC，DD₁所在直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系.若平面MCA₁的一个法向量为n=(1，2，1)，则 $\frac{A M}{M B}$ 等于

A: $\frac{1}{3}$
B: $\frac{1}{2}$
C: $\frac{2}{3}$
D: 1

解析:

设AM=x，则A₁(4，0，2)，M(4，x，0) $， \vec{A_{1} M}$ =(0，x，-2)，

因为平面MCA₁的一个法向量为n=(1，2，1)，则n· $\vec{A_{1} M}$ =0，即2x-2=0，解得x=1，

故AM=1，MB=3-1=2，故 $\frac{A M}{M B}$ = $\frac{1}{2}$ .

第16题 (填空题) 难度 - 基础题：

已知在空间直角坐标系中，A(2，0，0)，B(0，3，0)，C(0，0，6)，点M(x，y，2)(x>0，y>0)在平面ABC内，则 $\frac{1}{x}$ + $\frac{1}{y}$ 的最小值为　　　　.

答案:

$\frac{5 + 2 \sqrt{6}}{4}$

解析:

依题意 $， \vec{A B}$ =(-2，3，0) $， \vec{B C}$ =(0，-3，6) $， \vec{A M}$ =(x-2，y，2)，

设平面ABC的法向量为m=(a，b，c)，

则 $\{\begin{array}{l} m \cdot \vec{A B} = - 2 a + 3 b = 0, \\ m \cdot \vec{B C} = - 3 b + 6 c = 0, \end{array}$

令c=1，得m=(3，2，1)，

依题意，m· $\vec{A M}$ =0，则3x+2y=4，

则 $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{1}{4}$ (3x+2y) $(\frac{1}{x} + \frac{1}{y})$

= $\frac{1}{4} (5 + \frac{2 y}{x} + \frac{3 x}{y}) \geq \frac{1}{4} (5 + 2 \sqrt{\frac{2 y}{x} \cdot \frac{3 x}{y}})$ = $\frac{5 + 2 \sqrt{6}}{4} ，$

当且仅当x=4- $\frac{4 \sqrt{6}}{3} ，$ y=2 $\sqrt{6}$ -4时取等号.

第一章 作业6 空间中点、直线和平面的向量表示

第一章作业6 空间中点、直线和平面的向量表示