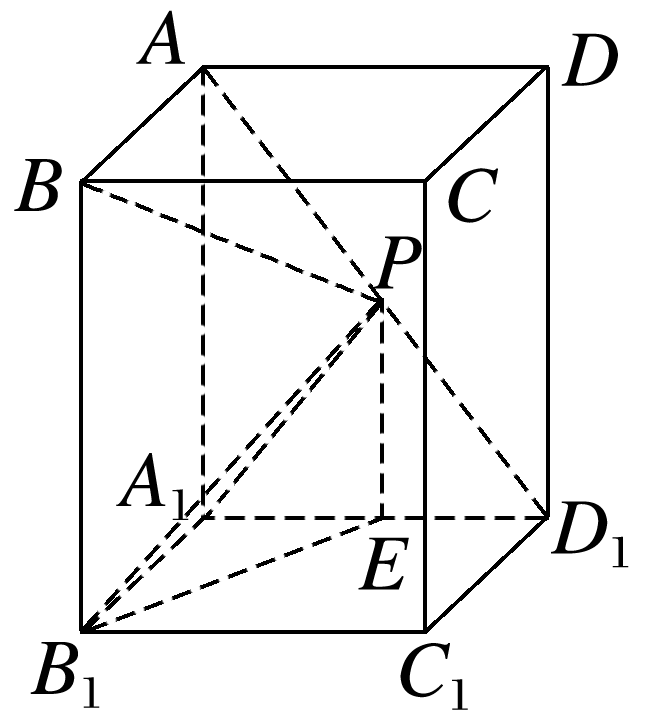
设D,E为正三角形ABC中BC边上的两个三等分点,且BC=2,则·等于
- A:
- B:
- C:
- D:
如图,
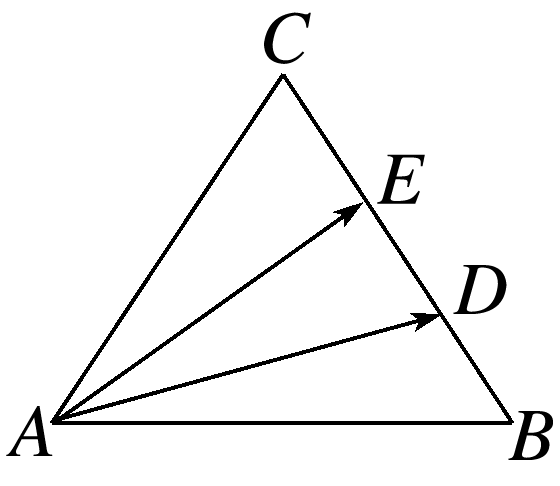
||=||=2,〈,〉=60°,
∵D,E是边BC上的两个三等分点,∴·
=·
=·
=||2+·+||2=×4+×2×2×+×4=.
若复数z满足i·z=3-4i,则|z|等于
方法一 依题意可得z===-4-3i,所以|z|==5.
方法二 依题意可得i2·z=(3-4i)i,所以z=-4-3i,则|z|==5.
某团队共有20人,他们的年龄分布如表所示.
年龄 | 28 | 29 | 30 | 32 | 36 | 40 | 45 |
人数 | 1 | 3 | 3 | 5 | 4 | 3 | 1 |
有关这20人年龄的众数、极差、百分位数说法不正确的是
年龄为32的有5人,故众数是32,A正确,B错误;
45-28=17,极差为17,C正确;
因为20×25%=5,所以(30+30)÷2=30,故25%分位数是30,D正确.
从装有10个红球和10个白球的罐子里任取两球,下列情况中互斥而不对立的两个事件是
对于A,“至少有一个红球”可能为一个红球、一个白球,“至少有一个白球”也可能为一个白球、一个红球,故两事件可能同时发生,所以不是互斥事件;对于B,“恰有一个红球”,则另一个必是白球,与“都是白球”是互斥事件,而任取两球还可能都是红球,故两事件不是对立事件;对于C,“至少有一个红球”为都是红球或一红一白,与“都是白球”显然是对立事件;对于D,“至多有一个红球”为都是白球或一红一白,与“都是红球”是对立事件.
对于两个平面α,β和两条直线m,n,下列命题中的真命题是
A中,n可能在α内,A是假命题;B中,m也可能在β内,B是假命题;C中,m与n可能平行、相交或异面,C是假命题;D中,m⊥α,α⊥β,则m⊂β或m∥β,若m⊂β,则由n⊥β得n⊥m,若m∥β,则β内有直线c∥m,而易知c⊥n,从而m⊥n,D是真命题.
设D,E为正三角形ABC中BC边上的两个三等分点,且BC=2,则·等于
如图,

||=||=2,〈,〉=60°,
∵D,E是边BC上的两个三等分点,∴·
=·
=·
=||2+·+||2=×4+×2×2×+×4=.
某校为了了解学生的视力情况,随机抽查了100名学生,得到如图所示的频率分布直方图.由于不慎将部分数据丢失,但知道前4组的频数和为40,后6组的频数和为87.设最大频率为a,视力在4.5到5.2之间的学生人数为b,则a,b的值分别为
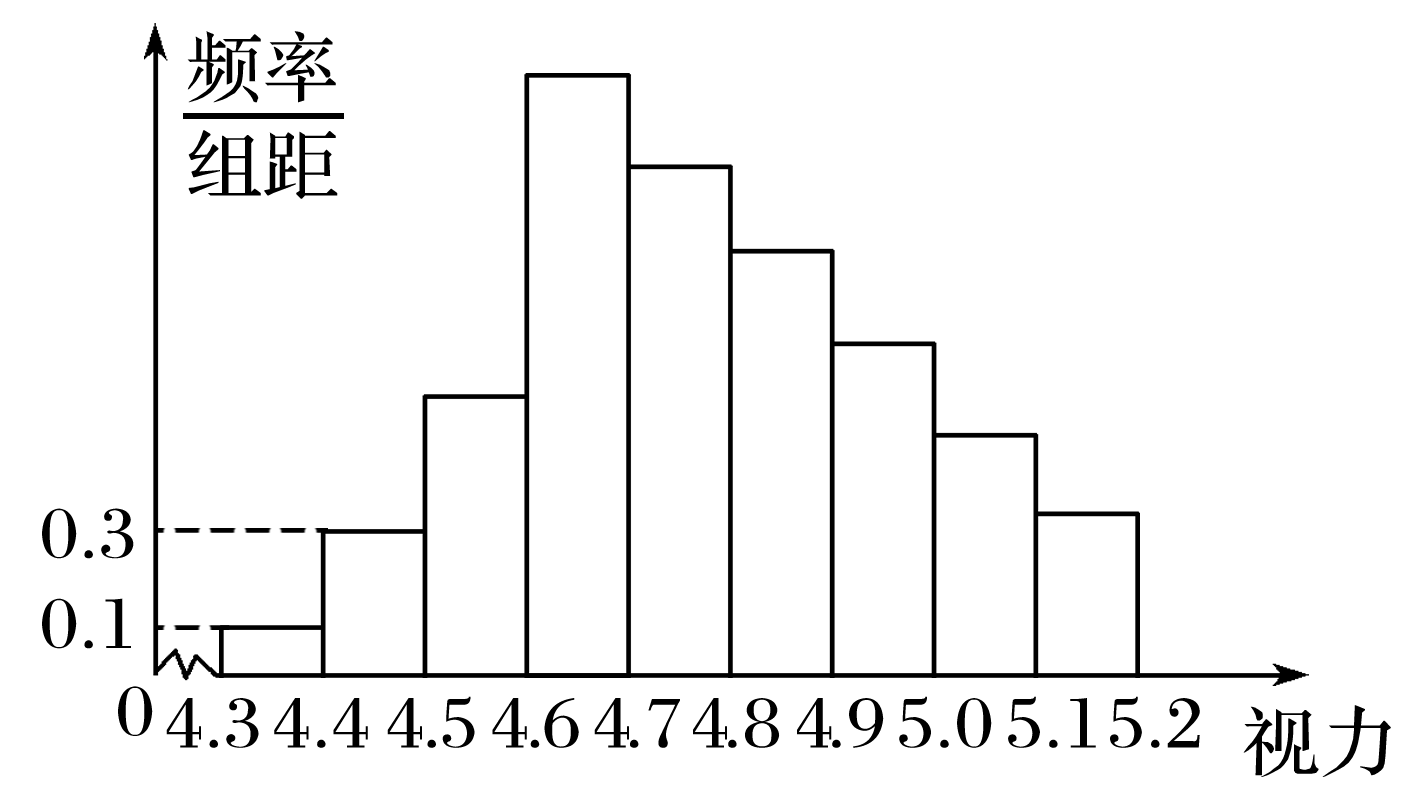
由频率分布直方图知组距为0.1,由前4组的频数和为40,后6组的频数和为87,知第4组的频数为40+87-100=27,即视力在4.6到4.7之间的频数为27,是最大频数,故最大频率a=0.27.视力在4.5到5.2之间的频率为1-0.01-0.03=0.96,故视力在4.5到5.2之间的学生人数b=0.96×100=96(人).
已知△ABC中,·=-3,AB=2,cos2A+sin2B+sin2C+sin Bsin C=1,D是边BC上一点,∠CAD=3∠BAD,则AD等于
设△ABC中,角A,B,C的对边为a,b,c,
∵cos2A+sin2B+sin2C+sin Bsin C=1,
即sin2B+sin2C+sin Bsin C=sin2A,
∴b2+c2+bc=a2,
∴cos A==-,
又A∈(0,π),∴A=,
又·=-3,AB=c=2,
∴·=2bcos A=2b×=-3,
即b=3,∴a2=b2+c2+bc=32+22+3×2=19,
故a=,
∴cos C===,
∵C∈,
∴sin C==,tan C=,
又∠CAD=3∠BAD,A=,
∴∠CAD=,AD=ACtan C=3×=.
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交棱AA1于点E,交棱CC1于点F,得四边形BFD1E,在以下结论中,不正确的是
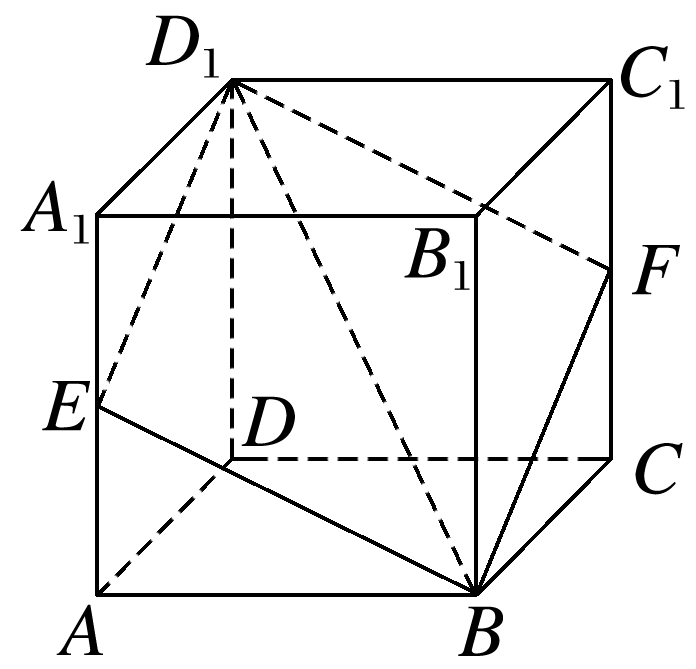
对于选项A,四边形BFD1E在底面ABCD内的投影一定是正方形ABCD,因此A正确;
对于选项B,当点E,F分别为AA1,CC1的中点时,
EF⊥平面BB1D1D,
又EF⊂平面BFD1E,
则平面BFD1E⊥平面BB1D1D,因此B正确;
对于选项C,因为平面ABB1A1∥平面DCC1D1,
且平面BFD1E∩平面ABB1A1=BE.
平面BFD1E∩平面DCC1D1=D1F,
所以BE∥D1F,同理D1E∥BF,
故四边形BFD1E为平行四边形,因此C错误;
对于选项D,当点F到线段BD1的距离最小时,
此时平行四边形BFD1E的面积最小,
此时点E,F分别为AA1,CC1的中点,
此时最小值为××=,因此D正确.
(多选)已知复平面内表示复数z=m+1+(m-1)i(m∈R)的点为M,则下列结论中正确的为
对于A,若z∈R,
则m-1=0,得m=1,故A错误;
对于B,因为M(m+1,m-1)在直线y=2x上,
所以m-1=2(m+1),
则m=-3,故B错误;
对于C,若z为纯虚数,则m+1=0,
即m=-1,此时虚部不为0,故C正确;
对于D,若M(m+1,m-1)在第四象限,
则
解得-1<m<1,故D正确.
(多选)如图所示,AB是半圆O的直径,VA垂直于半圆O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是
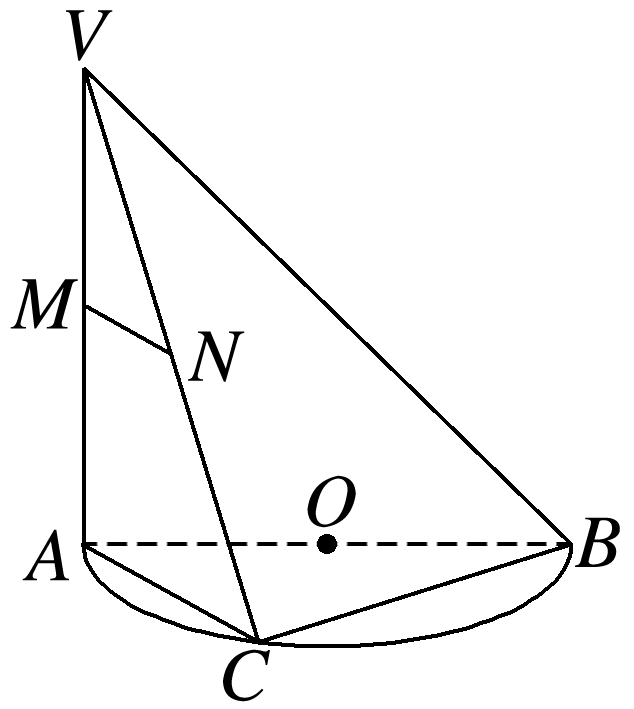
对于A,连接OC(图略),因为AB是半圆O的直径,所以AC⊥BC,所以OC与AC不垂直,
因为AC⊂平面VAC,
所以OC与平面VAC不可能垂直,所以A错误;
对于B,因为M,N分别为VA,VC的中点,所以MN∥AC,
因为MN⊄平面ABC,AC⊂平面ABC,
所以MN∥平面ABC,所以B正确;
对于C,由选项B可知MN∥AC,
所以∠ACB为MN与BC所成的角,
因为AC⊥BC,
所以MN与BC所成的角为90°,所以C正确;
对于D,因为VA⊥平面ABC,
BC⊂平面ABC,所以VA⊥BC,
因为AC⊥BC,VA∩AC=A,
VA,AC⊂平面VAC,所以BC⊥平面VAC,
因为BC⊂平面VBC,
所以平面VAC⊥平面VBC,所以D正确.
(多选)设点D是△ABC所在平面内一点,则下列说法正确的有
对于A,∵=+),
即-=-,即=,
即点D是边BC的中点,故A正确;
对于B,·==(-||+||)=0,即AD⊥BC,
故直线AD过△ABC的垂心,故B正确;
对于C,∵=2-,
即-=-,即=,
即点D在边CB的延长线上,故C错误;
对于D,∵=x+y,且x+y=,
设=2,则=2=2x+2y,且2x+2y=1,
故M,B,C三点共线,且||=2||,
即△BCD的面积是△ABC的面积的一半,故D正确.
已知向量a=(x,2),b=(2,1),c=(3,x),若a∥b,则|b+c|= .
答案: 5
因为a∥b,
所以x-2×2=0,解得x=4,
则 b+c=(2,1)+(3,4)=(5,5),
所以|b+c|=5.
若圆锥的底面半径为4,其侧面展开图的面积为20π,则该圆锥的高为 .
答案: 3
设该圆锥的母线长为l,高为h,
圆锥的侧面积为π×4×l=20π,可得l=5,
因此该圆锥的高为h===3.
在抛掷一枚质地均匀的骰子的试验中,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则在一次试验中,事件A∪发生的概率为 .
答案:
掷一枚骰子的试验有6种等可能的结果,依题意知P(A)==,P(B)==,
所以P()=1-P(B)=1-=,
因为表示“出现5点或6点”的事件,所以事件A与互斥,从而P(A∪)=P(A)+P()=+=.
已知|a|=2,|b|=4,且|a+b|=2.
(1)求a与b的夹角;
(2)若(2a-b)⊥(a+kb),求实数k的值.
答案: 解 (1)因为|a+b|2=a2+2a·b+b2=4+2a·b+16=12, 所以a·b=-4. 设a与b的夹角为θ,θ∈[0,π], 则cos θ===-, 又θ∈[0,π], 所以θ=, 故a与b的夹角为. (2)因为(2a-b)⊥(a+kb), 所以(2a-b)·(a+kb)=0, 即2a2+2ka·b-a·b-kb2=0, 即2|a|2+2ka·b-a·b-k|b|2=0, 所以8-8k+4-16k=0, 即12-24k=0, 解得k=.
记△ABC的内角A,B,C的对边分别为a,b,c,已知sin Csin(A-B)=sin Bsin(C-A).
(1)证明:2a2=b2+c2;
(2)若a=5,cos A=,求△ABC的周长.
答案: (1)证明 因为sin Csin(A-B)=sin Bsin(C-A), 所以sin Csin Acos B-sin Csin Bcos A =sin Bsin Ccos A-sin Bsin Acos C, 所以ac·-2bc·=-ab·, 即-=-, 所以2a2=b2+c2. (2)解 因为a=5,cos A=, 由(1)得b2+c2=50, 由余弦定理可得a2=b2+c2-2bccos A, 则50-bc=25, 所以bc=, 故(b+c)2=b2+c2+2bc=50+31=81, 所以b+c=9, 所以△ABC的周长为a+b+c=14.
某高校的特殊类型招生面试中有4道题目,获得面试资格的甲同学对一~四题回答正确的概率依次是,,,.规定按照题号依次作答,并且答对一,二,三,四题分别得1,2,3,6分,答错1题减2分,当累计积分小于-2分时面试失败,不少于4分时通过面试,假设甲同学每题回答正确与否相互之间没有影响.
(1)求甲同学回答完前3题即通过面试的概率;
(2)求甲同学最终通过面试的概率.
答案: 解 (1)设事件Mi(i=1,2,3,4)表示“甲同学第i个问题回答正确”, 记“甲同学回答完前3题即通过面试”为事件Q1, 则Q1=M1M2M3, 则P(Q1)=P(M1M2M3)=××=, 故甲同学回答完前3题即通过面试的概率为. (2)记“甲同学最终通过面试”为事件Q2,则 Q2=M1M2M3+M2M3M4+M1M3M4+M1M2M4+M2M4, 故P(Q2)=P(M1M2M3+M2M3M4+M1M3M4+M1M2M4+M2M4) =××+×××+×××+×××+××× =++++=. 故甲同学最终通过面试的概率为.
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
(1)为了调查评委对7位歌手的支持情况,现用按比例分配的分层随机抽样的方法从各组中抽取若干评委,其中从B组抽取了6人,请将其余各组抽取的人数填入下表.
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
抽取人数 | 6 |
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
答案: 解 (1)由题设知,比例分配的分层随机抽样的抽样比为6%,所以各组抽取的人数如下表. 组别 A B C D E 人数 50 100 150 150 50 抽取人数 3 6 9 9 3 (2)记从A组抽到的3位评委分别为a1,a2,a3,其中a1,a2支持1号歌手;从B组抽到的6位评委分别为b1,b2,b3,b4,b5,b6,其中b1,b2支持1号歌手,从{a1,a2,a3}和{b1,b2,b3,b4,b5,b6}中各抽取1人的所有样本点如图: 由树状图知所有样本点共18个,且是等可能的,其中2人都支持1号歌手的有a1b1,a1b2,a2b1,a2b2,共4个, 故所求概率P==.
undefined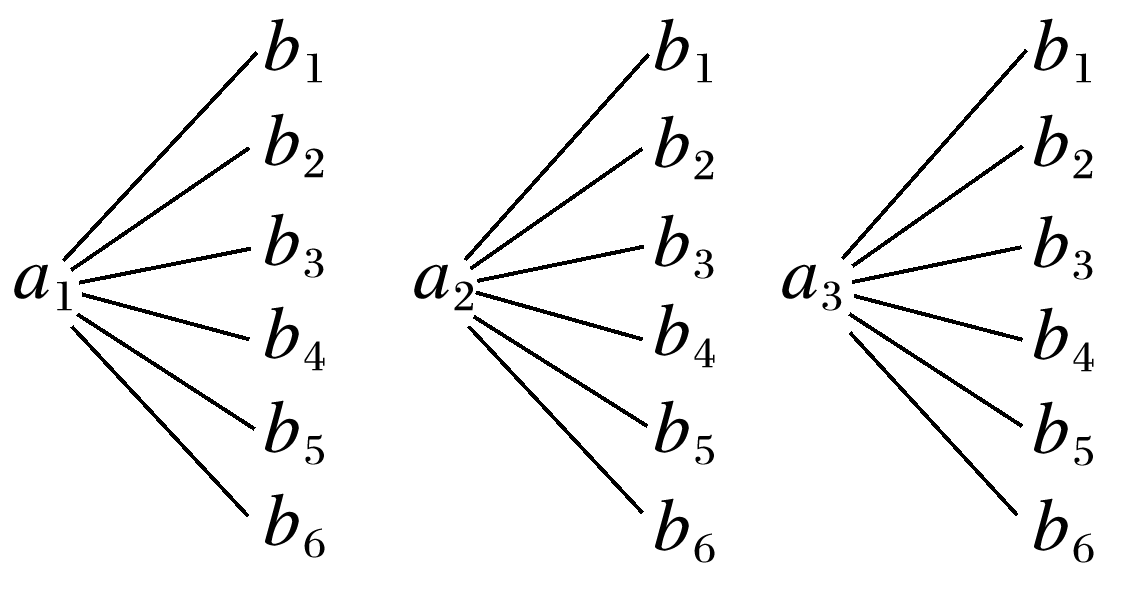
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.
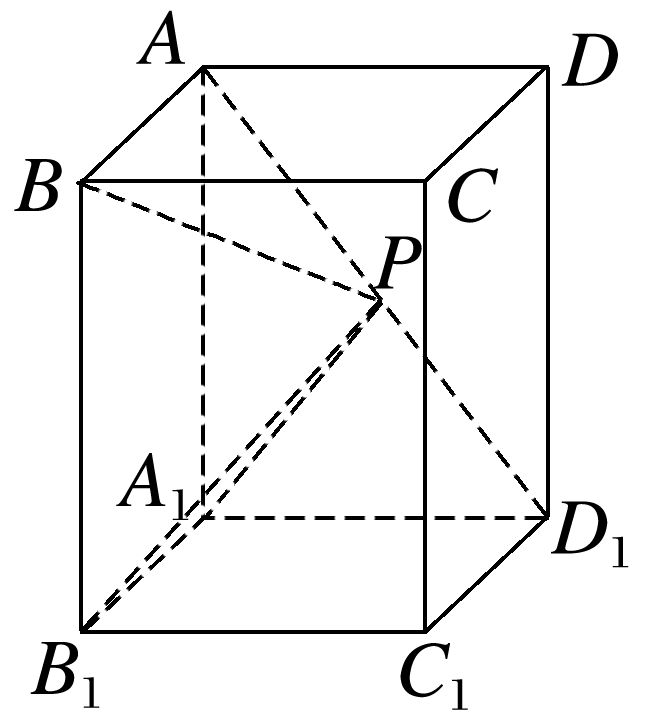
(1)试判断不论点P在AD1上的任何位置,是否都有平面BPA⊥平面AA1D1D,并证明你的结论;
(2)当P为AD1的中点时,求异面直线AA1与B1P所成角的余弦值;
(3)求PB1与平面AA1D1D所成角的正切值的最大值.
答案: 解 (1)是.∵BA⊥平面AA1D1D,BA⊂平面BPA, ∴平面BPA⊥平面AA1D1D, ∴无论点P在AD1上的任何位置,都有平面BPA⊥平面AA1D1D. (2)过点P作PE⊥A1D1,垂足为E,连接B1E,如图, 则PE∥AA1, ∴∠B1PE是异面直线AA1与B1P所成的角. 在Rt△AA1D1中,∵∠AD1A1=60°, ∴∠A1AD1=30°, ∴A1B1=A1D1=AD1=2, ∴A1E=A1D1=1,AA1=A1D1=2, ∴PE=AA1=,B1E==, ∴在Rt△B1PE中, B1P==2, ∴cos∠B1PE===, ∴异面直线AA1与B1P所成角的余弦值为. (3)由(1)知,B1A1⊥平面AA1D1D, ∴∠B1PA1是PB1与平面AA1D1D所成的角, ∴tan∠B1PA1==, ∴当A1P最小时,tan∠B1PA1最大, 这时A1P⊥AD1,A1P==, 得tan∠B1PA1=, 即PB1与平面AA1D1D所成角的正切值的最大值为.