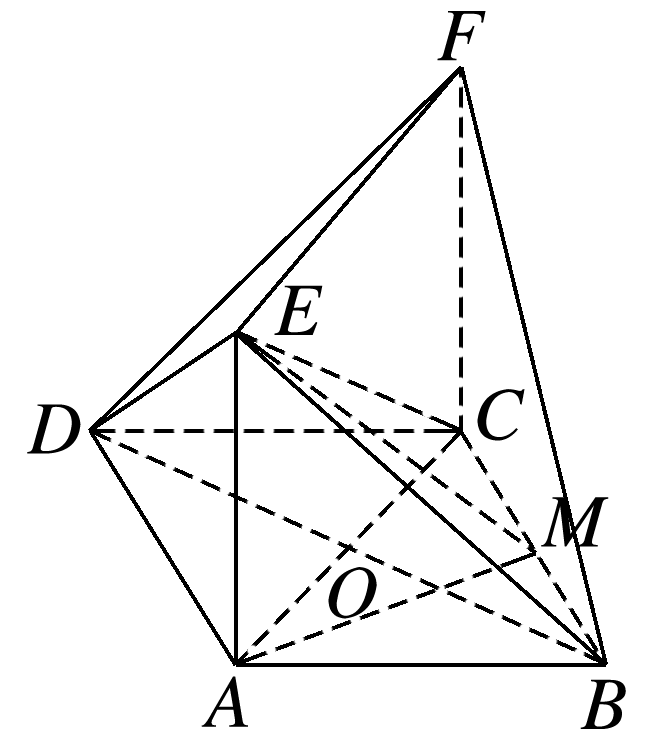
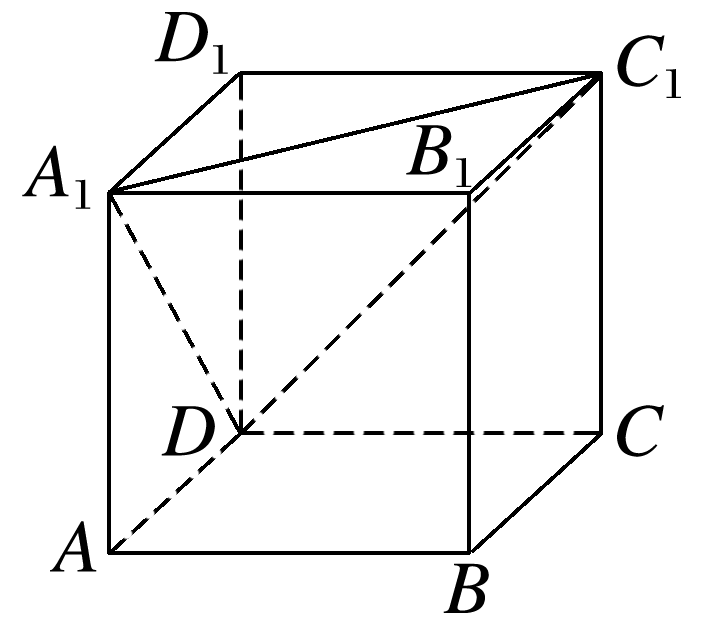
棱长为3的正方体ABCD-A1B1C1D1中,点D1到平面A1C1D的距离为( )
- A:
- B: 1
- C: 2
- D:
在正方体ABCD-A1B1C1D1中,
A1C1=A1D=C1D=3,
A1D2=,
令点D1到平面A1C1D的距离为h,
由,
得×h=××32×3,
解得h=,
所以点D1到平面A1C1D的距离为.
若l,m,n表示不重合的三条直线,α表示平面,则下列说法中正确的个数为( )
①l∥m,m∥n,l⊥α,则n⊥α;
②l∥m,m⊥α,n⊥α,则l∥n;
③m⊥α,n⊂α,则m⊥n.
①正确,∵l∥m,m∥n,∴l∥n.又l⊥α,∴n⊥α.②正确,∵l∥m,m⊥α,∴l⊥α.又n⊥α,∴l∥n.③正确,由线面垂直的定义可知其正确.故选D.
在圆柱的一个底面上任取一点(该点不在底面圆周上),过该点作另一个底面的垂线,则这条垂线与圆柱的母线所在直线的位置关系是( )
因为圆柱的母线垂直于圆柱的底面,由线面垂直的性质定理可得两直线平行.
棱长为3的正方体ABCD-A1B1C1D1中,点D1到平面A1C1D的距离为( )
在正方体ABCD-A1B1C1D1中,

A1C1=A1D=C1D=3,
A1D2=,
令点D1到平面A1C1D的距离为h,
由,
得×h=××32×3,
解得h=,
所以点D1到平面A1C1D的距离为.
在△ABC中,∠ACB=90°,AB=8,∠BAC=60°,PC⊥平面ABC,PC=4,M是AB边上的一动点,则PM的最小值为( )
如图所示,
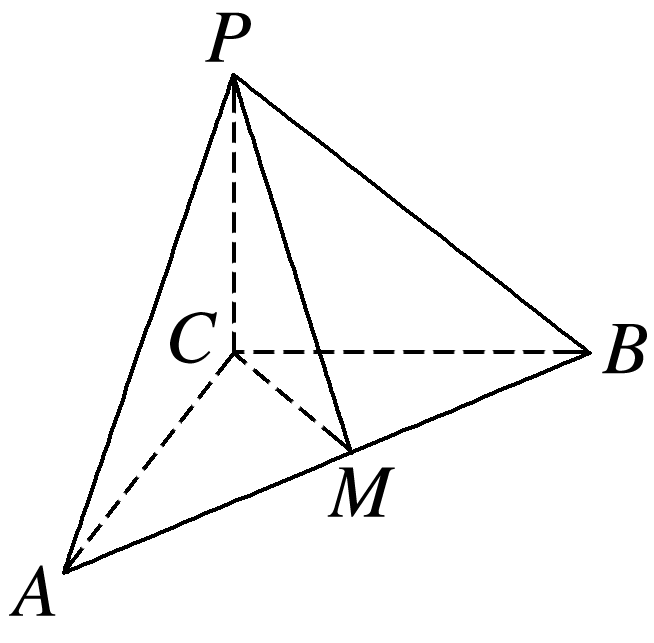
因为PC⊥平面ABC,所以PC⊥CM,则△PCM是直角三角形,故PM2=PC2+CM2,所以当CM⊥AB时,CM最小,此时PM也最小.由条件知AC=4,BC=4,
因为AB=8,
故CM的最小值为=2,
又PC=4,
则PM的最小值为=2.
点P不在△ABC所在平面上,过P作平面α,使△ABC的三个顶点到α的距离相等,这样的平面α共有( )
若过点P的平面恰好过△ABC某两边的中点,此时满足△ABC的三个顶点到平面α的距离相等,则这样的平面有3个,若过点P的平面与△ABC所在的平面平行,此时满足△ABC的三个顶点到平面α的距离相等,则这样的平面只有1个,综上,符合条件的平面α共有4个.
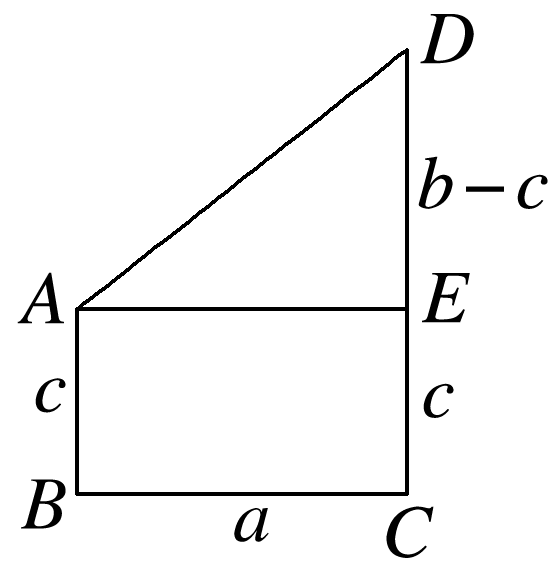
地面上有两根相距a米的旗杆,它们的高分别是b米和c米(b>c),则它们上端的距离为( )
如图,由线面垂直的性质定理可知AB∥CD,过点A作AE⊥CD于点E,则DE=b-c,故AD=.
已知平面α和两条不同的直线m,n,下面的条件中一定可以推出m⊥n的是( )
对选项A,若m⊥α,n∥α,则存在直线b⊂α,且n∥b,因为m⊥α,b⊂α,所以m⊥b,即m⊥n,故A正确;
对选项B,若m⊥α,n⊥α,则m∥n,故B错误;
对选项C,m⊂α,n⊥α,则m⊥n,故C正确;
对选项D,若m∥α,n∥α,则m,n的位置关系为平行、相交或异面,故D错误.
如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.下列结论中正确的是( )
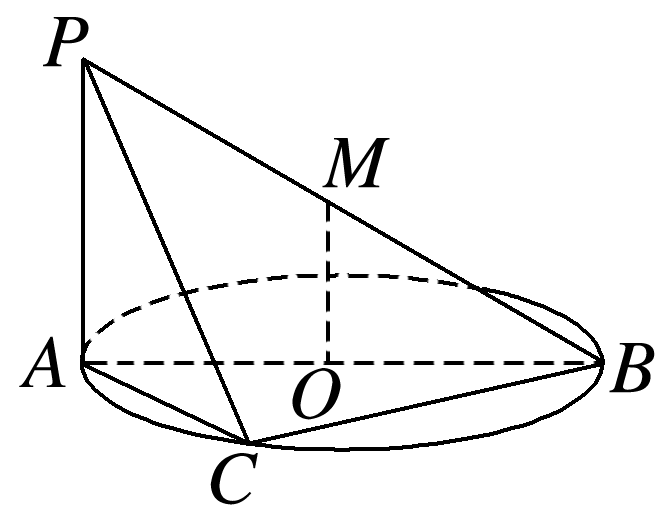
对于A,∵直线PA垂直于圆O所在的平面,∴PA⊥BC.
∵AB为圆O的直径,∴AC⊥BC,又PA∩AC=A,PA,AC⊂平面PAC,
∴BC⊥平面PAC,又PC⊂平面PAC,∴BC⊥PC,A正确;
对于B,∵点M为线段PB的中点,点O为直径AB的中点,∴OM∥PA.又PA⊂平面PAC,OM⊄平面PAC,∴OM∥平面PAC,B正确;
对于C,∵BC⊥平面PAC,∴点B到平面PAC的距离等于线段BC的长,C正确;
对于D,∵点M为线段PB的中点,∴点M到平面PAC的距离是点B到平面PAC距离的,
∴VM-PAC=VB-PAC,又VB-PAC=VP-ABC,
∴VM-PAC=VP-ABC,D不正确.
如图,等边三角形ABC的边长为1,BC边上的高为AD,沿AD把△ABC折起来,则下列结论正确的是( )
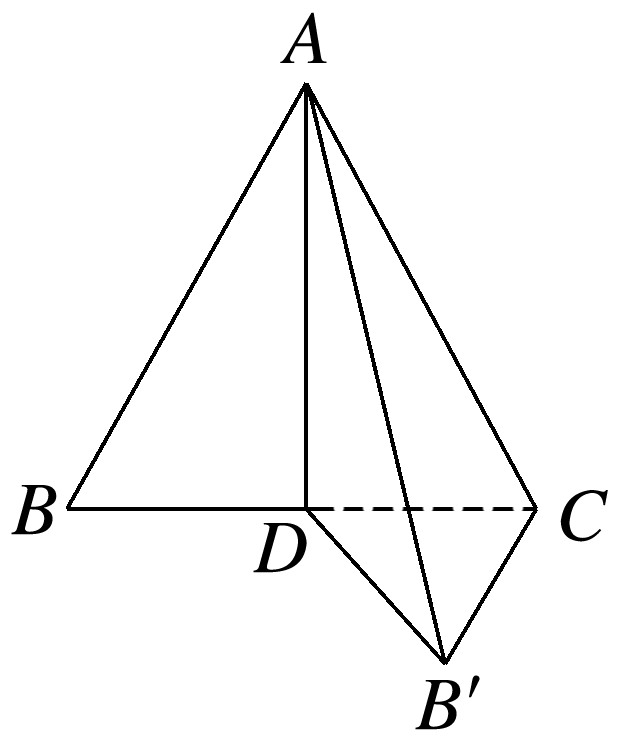
因为AD⊥DC,AD⊥DB',且DC∩DB'=D,DC,DB'⊂平面DB'C,所以AD⊥平面DB'C,故A正确;当DB'⊥DC时,△DB'C的面积最大,此时三棱锥A-DB'C的体积也最大,最大值为××××,故B错误;当∠B'DC=60°时,△DB'C是等边三角形,设B'C的中点为E,连接AE,DE(图略),
则AE⊥B'C,即AE为点A到B'C的距离,
AE=,故C正确;
当∠B'DC=90°时,CD⊥DB',CD⊥AD,AD∩DB'=D,AD,DB'⊂平面ADB',故CD⊥平面ADB',则CD就是点C到平面ADB'的距离,CD=,故D正确.
a,b是异面直线,直线l⊥a,l⊥b,直线m⊥a,m⊥b,则l与m的位置关系是 .
答案: 平行
将b平移至c,且使a与c相交,
则a,c确定一个平面,记作平面α.
∵l⊥b,m⊥b,
∴l⊥c,m⊥c,
又l⊥a,m⊥a,
∴l⊥平面α,m⊥平面α,
∴l∥m.
如图,正方体ABCD-A1B1C1D1的棱长为2,E,F,G,H分别是所在棱的中点,则平面EFGH与平面AB1C1D之间的距离为 .
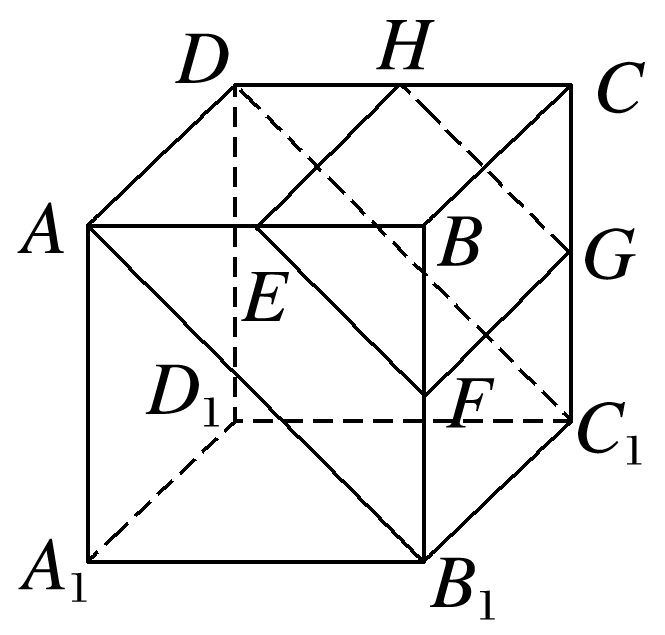
答案:
连接A1B,与AB1和EF分别交于点M,N(图略),
易证A1B与平面EFGH和平面AB1C1D都垂直,
则MN的长就是这两个平面之间的距离,
易求得MN=A1B=×2.
一条与平面α相交的线段AB,其长度为10 cm,两端点A,B到平面α的距离分别是3 cm,2 cm,则线段AB与平面α所成角的大小是 .
答案: 30°
如图,作AC⊥α,BD⊥α,垂足分别为C,D,则AC∥BD,AC,BD确定的平面与平面α交于CD,
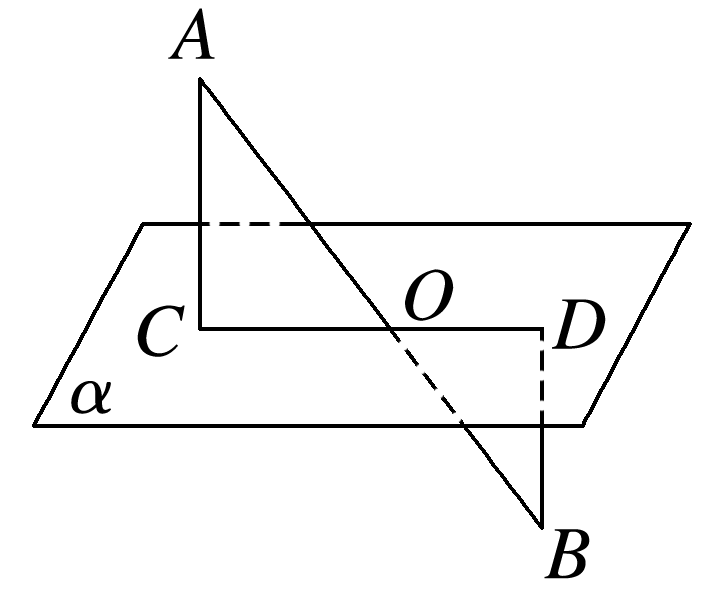
设CD与AB相交于O,则AB=10 cm,
AC=3 cm,BD=2 cm,
则AO=6 cm,BO=4 cm,
所以∠AOC=∠BOD=30°,即线段AB与平面α所成的角的大小为30°.
在正方体ABCD-A1B1C1D1各表面上的对角线中,与体对角线AC1垂直的面对角线共有 条.
答案: 6
如图所示,BD⊥AC,
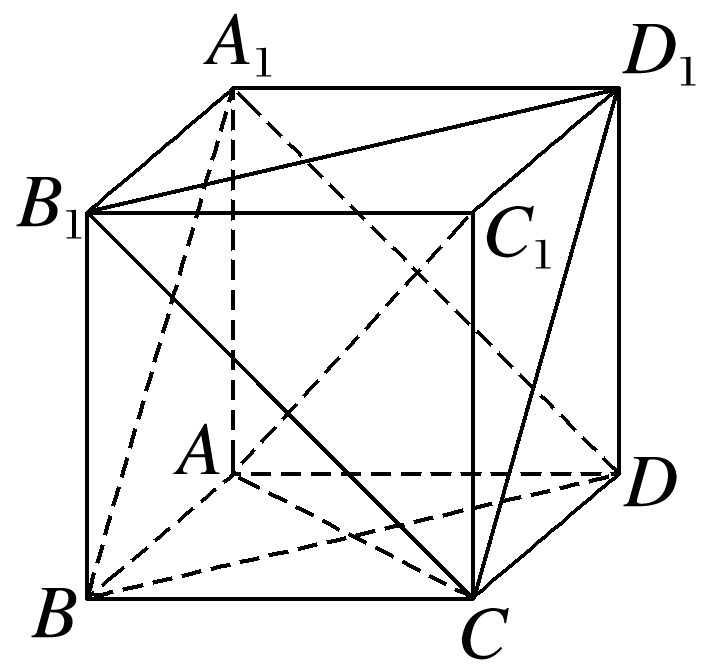
在正方体ABCD-A1B1C1D1中,CC1⊥平面BCD,BD⊂平面BCD,
所以CC1⊥BD,
又AC∩CC1=C,AC,CC1⊂平面ACC1,所以BD⊥平面ACC1,
又AC1⊂平面ACC1,所以AC1⊥BD.
同理可得,A1B,A1D,B1D1,D1C,B1C都与AC1垂直,共6条.
如图,已知平面α∩平面β=l,EA⊥α,垂足为A,EB⊥β,垂足为B,直线a⊂β,a⊥AB.求证:a∥l.
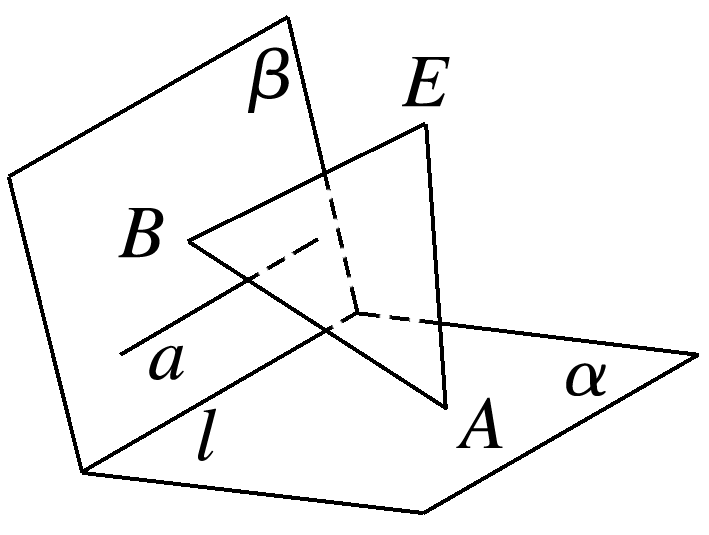
答案: 证明 因为EB⊥β,a⊂β,所以EB⊥a. 又因为a⊥AB,AB∩EB=B, AB,EB⊂平面ABE, 所以a⊥平面ABE. 因为α∩β=l,所以l⊂α,l⊂β. 因为EA⊥α,EB⊥β, 所以EA⊥l,EB⊥l. 又因为EA∩EB=E,EA,EB⊂平面ABE, 所以l⊥平面ABE.所以a∥l.
已知在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱A1D1,AD,C1D1的中点,求直线BB1到平面EFG的距离.
答案: 解 如图所示,连接B1D1,交A1C1于点O,交EG于点H. 由正方体的性质可知EF∥BB1,又EF⊂平面EFG,BB1⊄平面EFG,则BB1∥平面EFG,则直线BB1到平面EFG的距离即为点B1到平面EFG的距离.由题易得EF⊥平面A1B1C1D1,因为HB1⊂平面A1B1C1D1,所以EF⊥HB1,又A1C1⊥B1D1,EG∥A1C1,所以EG⊥HB1,又EG∩EF=E,EG,EF⊂平面EFG, 所以HB1⊥平面EFG, 故直线BB1到平面EFG的距离为HB1=B1D1=.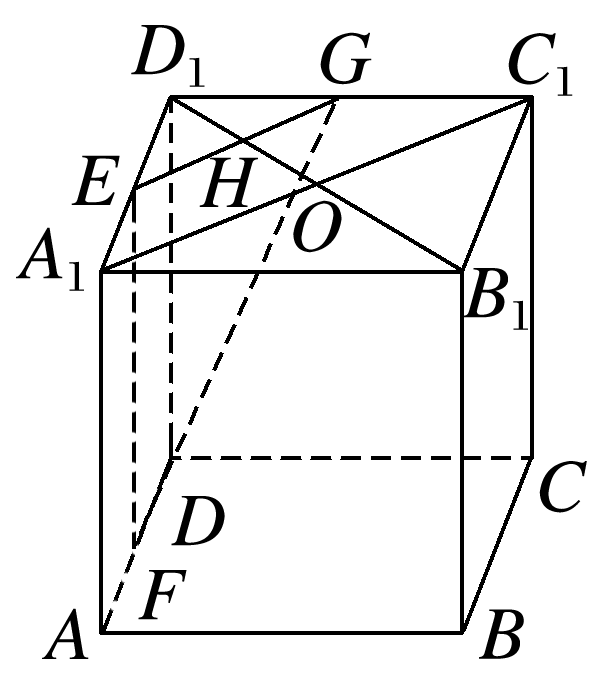
已知在正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2,E为CC1的中点,求直线AC1到平面BED的距离.
答案: 解 如图,连接AC交BD于点O,连接OE. 在△CC1A中,易证OE∥AC1.又OE⊂平面BED,AC1⊄平面BED,∴AC1∥平面BED,∴直线AC1到平面BED的距离为点A到平面BED的距离. 连接AE,V三棱锥E-ABD=S△ABD·EC=××2×2×. 在△BED中,BD=2,BE=,DE=, ∴S△BED=×2×=2. 设点A到平面BED的距离为h, 由V三棱锥A-BDE=V三棱锥E-ABD,得S△BED·h=×2×h=h=,解得h=1.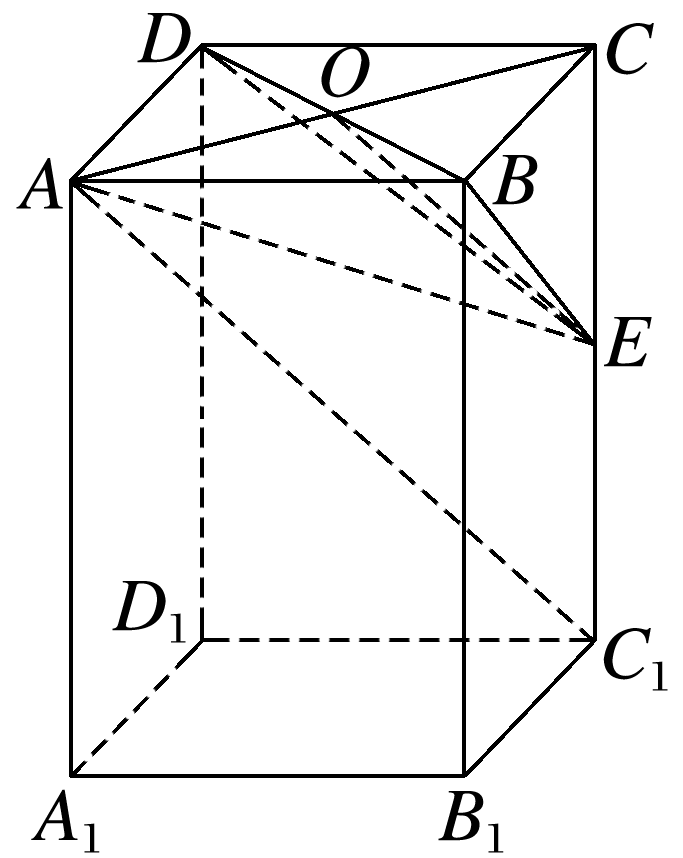
在棱长为1的正方体ABCD-A1B1C1D1中,点A到直线B1D1的距离为a,点A1到平面BDD1B1的距离为b,B1C1到平面A1D1CB的距离为c,平面AA1B1B到平面DD1C1C的距离为d.则以下关于a,b,c,d大小关系的叙述,正确的是( )
如图(1),连接B1D1交A1C1于M,
连接AM,由正方体的性质可知AB1=AD1,
M是B1D1的中点,
所以AM⊥B1D1,
又可求得AM=,
所以点A到直线B1D1的距离a=;
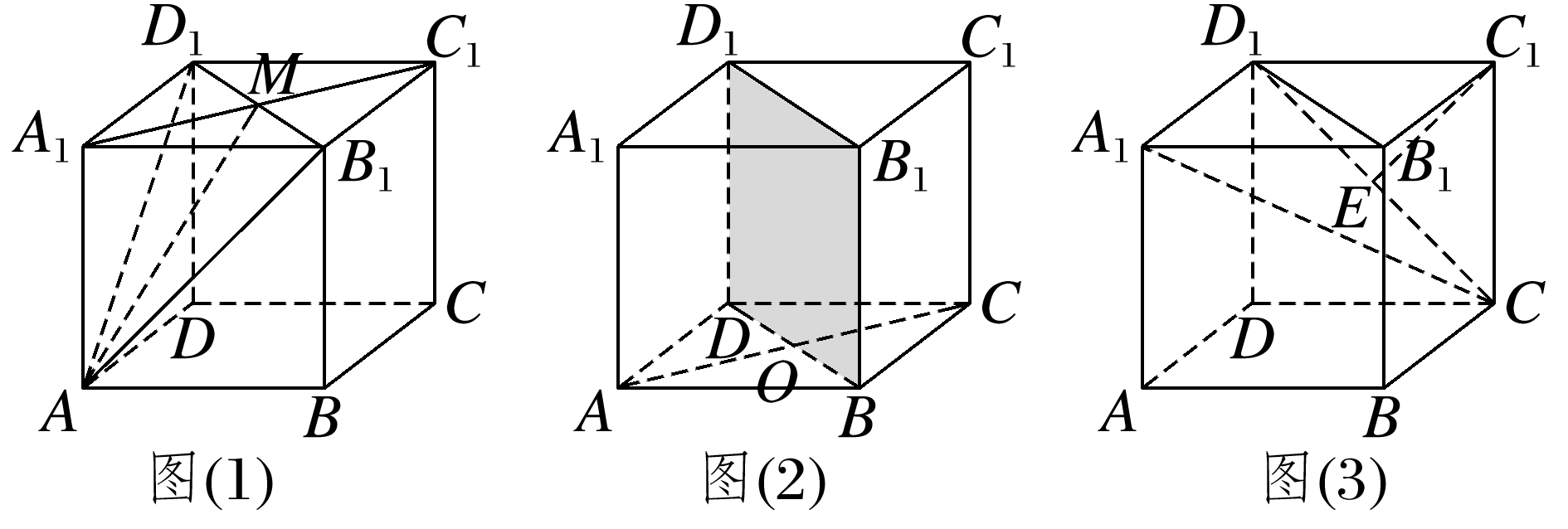
如图(2),连接AC交BD于点O,
因为四边形ABCD是正方形,所以AC⊥BD,
在正方体ABCD-A1B1C1D1中,
BB1⊥平面ABCD,故BB1⊥AC,
又BB1∩BD=B,BB1,BD⊂平面BDD1B1,
所以AC⊥平面BDD1B1,
故AO⊥平面BDD1B1,
易得AA1∥平面BDD1B1,
所以AO为点A1到平面BDD1B1的距离,
在正方形ABCD中,
可得b=AO=AC=;
如图(3),在棱长为1的正方体ABCD-A1B1C1D1中,
取CD1的中点E,连接C1E,
则C1E⊥CD1,且C1E=,
又A1D1⊥平面CDD1C1,
C1E⊂平面CDD1C1,
所以A1D1⊥C1E,
而A1D1∩CD1=D1,
所以C1E⊥平面A1D1C,
易知B1C1∥平面A1D1C,
则C1到平面A1D1C的距离即为直线B1C1到平面A1D1C的距离,
所以直线B1C1到平面A1D1CB的距离c=.
由正方体ABCD-A1B1C1D1的性质可得平面AA1B1B到平面DD1C1C的距离d=BC=1.
综上,a=,b=c=,d=1.
如图,在菱形ABCD中,∠ABC=60°,AC与BD相交于点O,EB=EC=ED,CF∥AE,AB=2,CF=3.
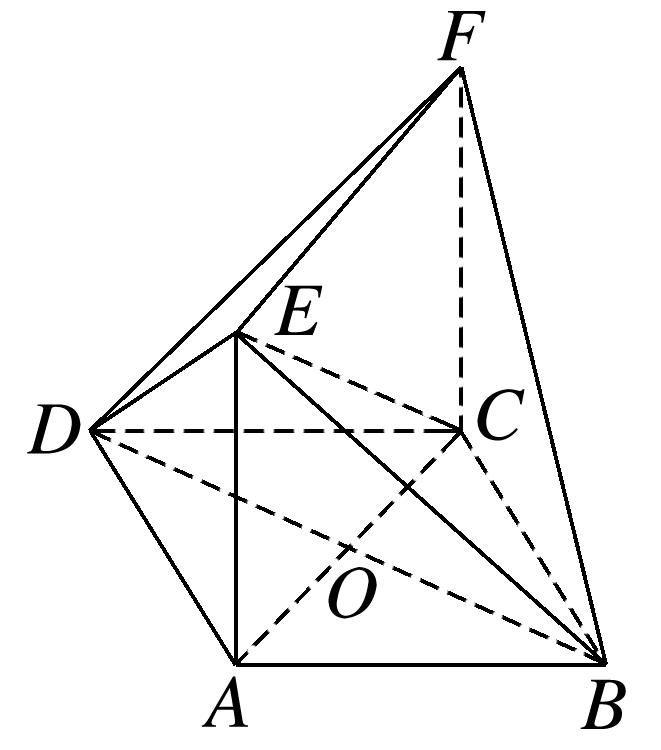
(1)求证:EA⊥平面ABCD;
(2)求四面体F-ECB的体积.
答案: (1)证明 在菱形ABCD中,∠ABC=60°,则△ABC和△ACD都是正三角形,取BC的中点M,连接EM,AM,如图所示. 因为M为BC的中点,所以BC⊥AM. 因为EB=EC,所以BC⊥ME, 又ME∩AM=M,AM,ME⊂平面MAE, 所以BC⊥平面MAE, 又AE⊂平面MAE,所以BC⊥EA. 同理可得CD⊥EA. 因为BC∩CD=C,BC,CD⊂平面ABCD, 所以EA⊥平面ABCD. (2)解 由(1)得EA⊥平面ABCD, 因为CF∥AE,所以CF⊥平面ABCD. 因为AM⊂平面ABCD,所以CF⊥AM. 又BC⊥AM,CF∩BC=C, CF,BC⊂平面FCB,所以AM⊥平面FCB. 由题意易得AM=, 又CF∥AE,CF⊂平面FCB,AE⊄平面FCB, 所以AE∥平面FCB,所以点E到平面FCB的距离等于点A到平面FCB的距离,即AM的长.故VF-ECB=VE-FCB=S△FCB·AM =××3×2×.