下列说法正确的是( )
- A: 多面体至少有3个面
- B: 有2个面平行,其余各面都是梯形的几何体是棱台
- C: 各侧面都是正方形的四棱柱一定是正方体
- D: 棱柱的侧棱相等,侧面是平行四边形
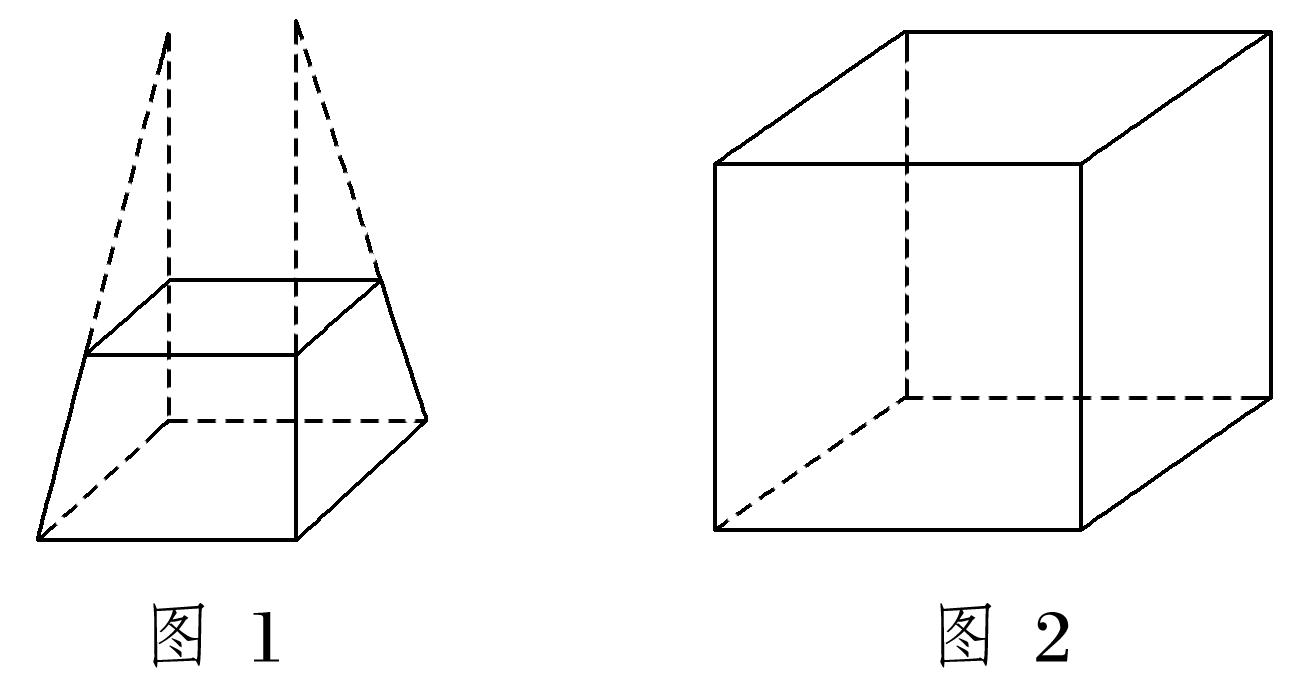
一个多面体至少有4个面,如三棱锥有4个面,不存在有3个面的多面体,所以选项A错误;选项B错误,反例如图1,各侧棱的延长线不能交于一点,则该几何体不是棱台;选项C错误,反例如图2,上、下底面是全等的菱形,各侧面是全等的正方形,它不是正方体;根据棱柱的定义可知选项D正确.
下列说法正确的是( )
一个多面体至少有4个面,如三棱锥有4个面,不存在有3个面的多面体,所以选项A错误;选项B错误,反例如图1,各侧棱的延长线不能交于一点,则该几何体不是棱台;选项C错误,反例如图2,上、下底面是全等的菱形,各侧面是全等的正方形,它不是正方体;根据棱柱的定义可知选项D正确.

已知水平放置的△ABC,按“斜二测画法”得到如图所示的直观图,其中B'O'=C'O'=1,A'O'=,那么原三角形ABC的面积是( )
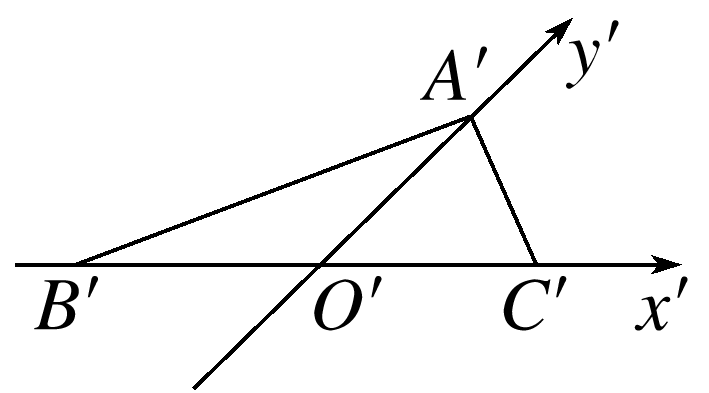
由斜二测画法的性质可得,BC=B'C'=2,AO=2A'O'=2×,由图易得AO⊥BC,
∴S△ABC=×2×.
若一个底面半径为1的圆锥侧面展开图是一个顶角为的扇形,则该圆锥的体积为( )
设圆锥的母线长为l,
由题意可得l=2π×1,解得l=3,
所以圆锥的高为h==2,
所以圆锥的体积为V=π×12×2π.
下列说法正确的是( )
两组对边分别相等的四边形可能是空间四边形,故A错误;
如图1,直线DD1与B1C1都是直线AB的异面直线,同样DD1与B1C1也是异面直线,故B错误;
如图2,设直线AB与CD是异面直线,则直线AC与BD一定不平行,否则,若AC∥BD,有AC与BD确定一个平面α,则AC⊂α,BD⊂α,所以A∈α,B∈α,C∈α,D∈α,所以AB⊂α,CD⊂α,这与假设矛盾,故C正确;
如图1,AB∥CD,而直线AA1与AB相交,但与直线CD不相交,故D错误.
如图所示,圆锥底面半径为1,母线AC=2,D为弧AB的中点,E是BC的中点,则异面直线AC与DE夹角的正弦值是( )
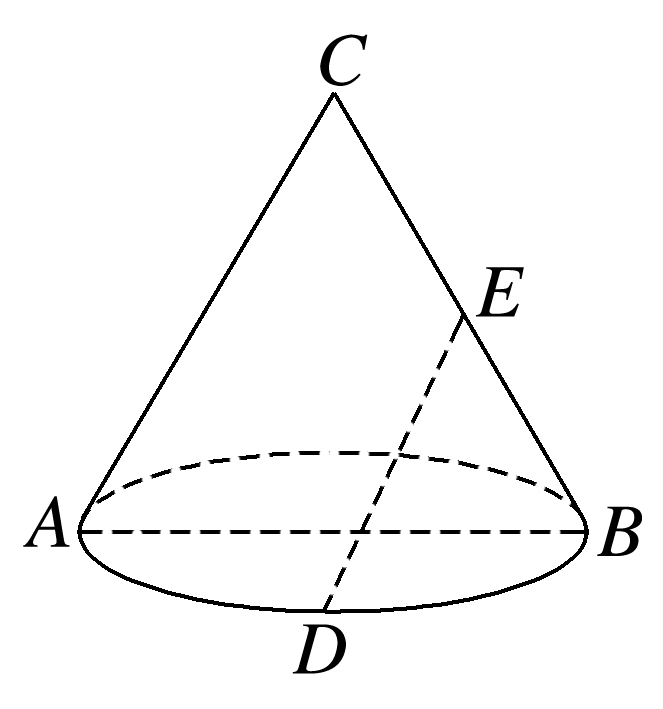
设底面圆心为O,
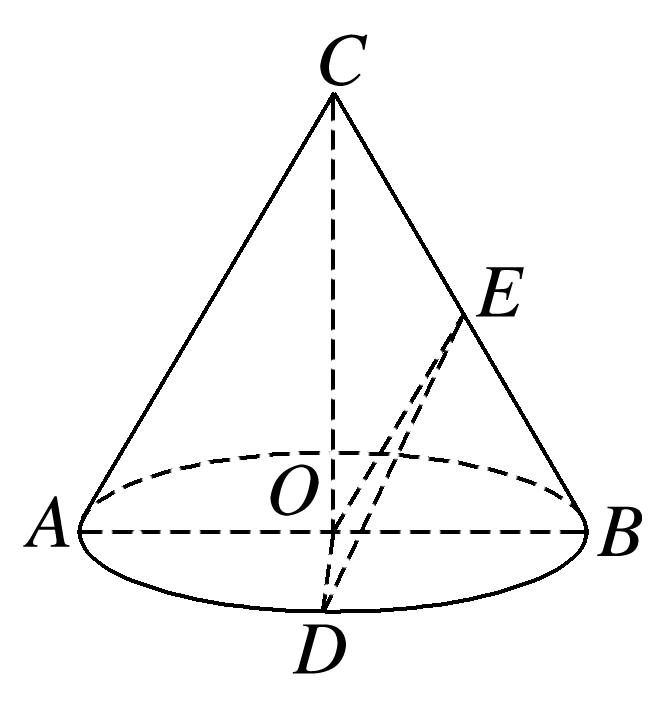
连接EO,CO,OD,
可知EO∥AC,
故∠OED为异面直线AC与DE所成的角(或其补角),
∵CO⊥底面ABD,∴CO⊥OD,
又点D为半圆弧AB的中点,
∴AB⊥OD.
又CO∩AB=O,CO,AB⊂平面ABC,
∴OD⊥平面ABC,又EO⊂平面ABC,
∴OD⊥EO.在Rt△ODE中,OD=OE=1,
∴∠OED=,∴sin∠OED=,
故异面直线AC与DE夹角的正弦值是.
在直三棱柱ABC-A1B1C1中,AC=4,AB=3,AA1=12,∠BAC=90°,且三棱柱的所有顶点都在同一球面上,则该球的表面积是( )
∵三棱柱ABC-A1B1C1的侧棱垂直于底面,
AC=4,AB=3,
∠BAC=90°,AA1=12,
∴可将棱柱ABC-A1B1C1补成长方体,
且长方体的长、宽、高分别为4,3,12.
∴长方体的体对角线长为=13,
即为球的直径.
∴球的表面积为S=4πR2=4π×=169π.
在正方体ABCD-A1B1C1D1中,下列说法正确的是( )
如图,在正方体ABCD-A1B1C1D1中,异面直线A1C1与AD所成的角为45°,故A错误;直线D1C1与直线AB平行,故B错误;异面直线AC1与DC所成的角为∠C1AB,
其正切值为≠1,所以异面直线AC1与DC所成的角不是45°,故C错误;连接A1D,DC1,因为A1D∥B1C,所以异面直线A1C1与B1C所成的角就是直线A1C1与直线A1D所成的角,而△A1DC1是等边三角形,
所以∠C1A1D=60°,
即A1C1与B1C所成的角为60°,故D正确.
如图,在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC,SA交于点D,E,F,H,且D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为( )
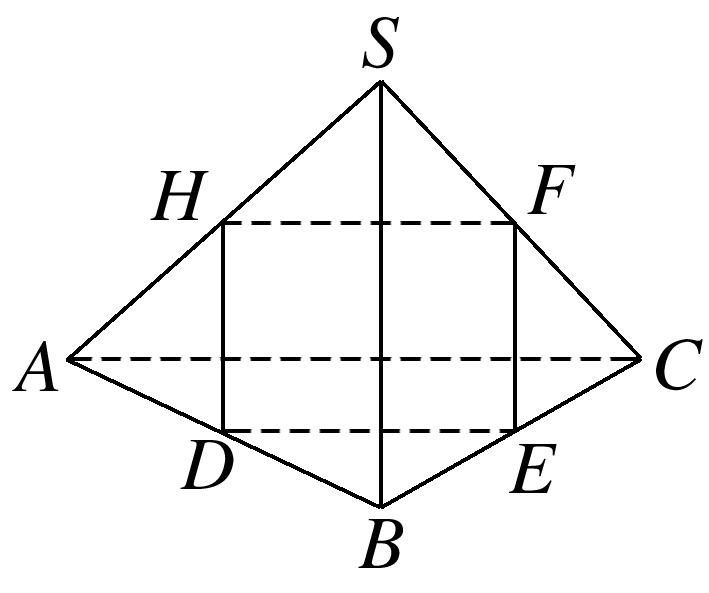
如图,取AC的中点G,连接SG,BG.
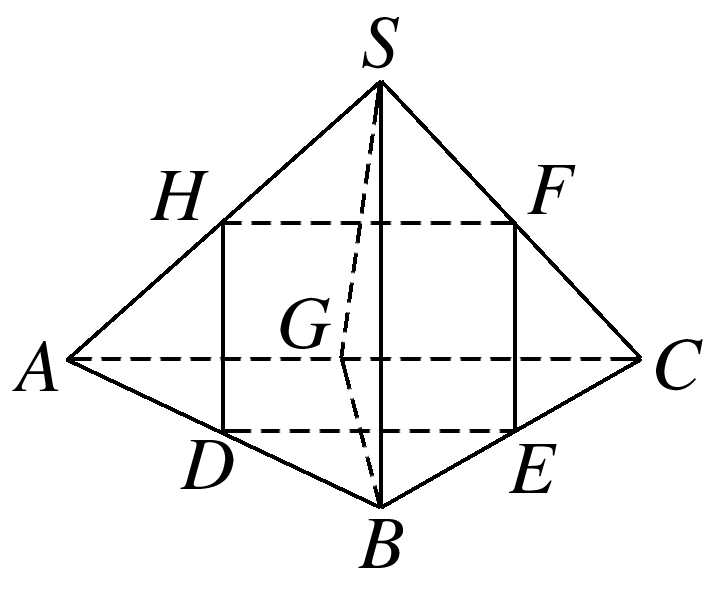
易知SG⊥AC,BG⊥AC,且SG∩BG=G,SG,BG⊂平面SGB,
故AC⊥平面SGB,
又SB⊂平面SGB,
所以AC⊥SB.因为SB∥平面DEFH,SB⊂平面SAB,平面SAB∩平面DEFH=HD,所以SB∥HD.同理SB∥FE.又D,E分别为AB,BC的中点,则H,F也分别为AS,SC的中点,从而得HF![]() AC
AC![]() DE,所以四边形DEFH为平行四边形.又AC⊥SB,SB∥HD,DE∥AC,所以DE⊥HD,所以四边形DEFH为矩形,其面积S=HF·HD=AC·SB=.
DE,所以四边形DEFH为平行四边形.又AC⊥SB,SB∥HD,DE∥AC,所以DE⊥HD,所以四边形DEFH为矩形,其面积S=HF·HD=AC·SB=.
已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,若直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列结论正确的是( )
因为m∥α,m∥β,α∩β=l,所以m∥l,又AB∥l,所以AB∥m,故A正确;因为AC⊥l,m∥l,所以AC⊥m,故B正确;因为A∈α,AB∥l,l⊂α,所以B∈α,所以AB⊄β,又l⊂β,所以AB∥β,故C正确;因为AC⊥l,当点C在α内时,AC⊥β成立,当点C不在α内时,AC⊥β不成立,故D不正确.
如图,四边形ABCD是圆柱的轴截面,E是底面圆周上异于A,B的一点,则下列结论中正确的是( )
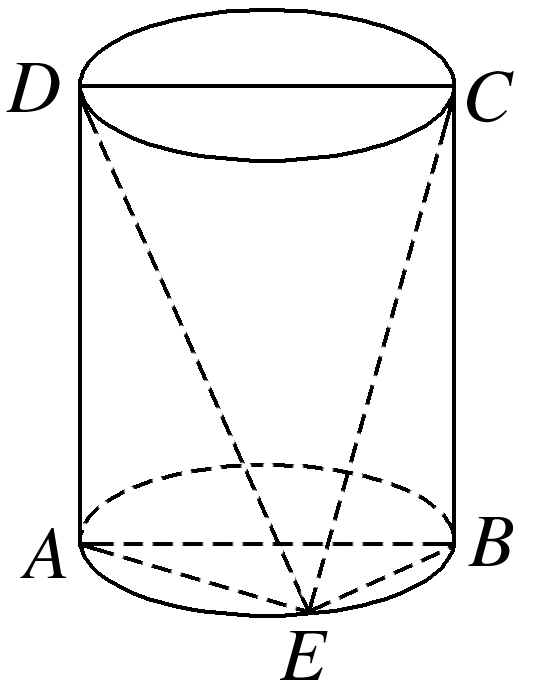
由AB是底面圆的直径,知∠AEB=90°,
即AE⊥EB.
∵四边形ABCD是圆柱的轴截面,
∴AD⊥底面AEB,BC⊥底面AEB.
又BE⊂平面AEB,∴AD⊥BE,
又AD∩AE=A,AD,AE⊂平面ADE,
∴BE⊥平面ADE,∵DE⊂平面ADE,
∴BE⊥DE.同理可得AE⊥CE.
又BE⊂平面BCE,∴平面BCE⊥平面ADE.
可得A,B,D正确.若DE⊥平面CEB,
则DE⊥BC,显然不成立,C错误.
如图,在棱长均相等的正四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,则下列结论中正确的是( )
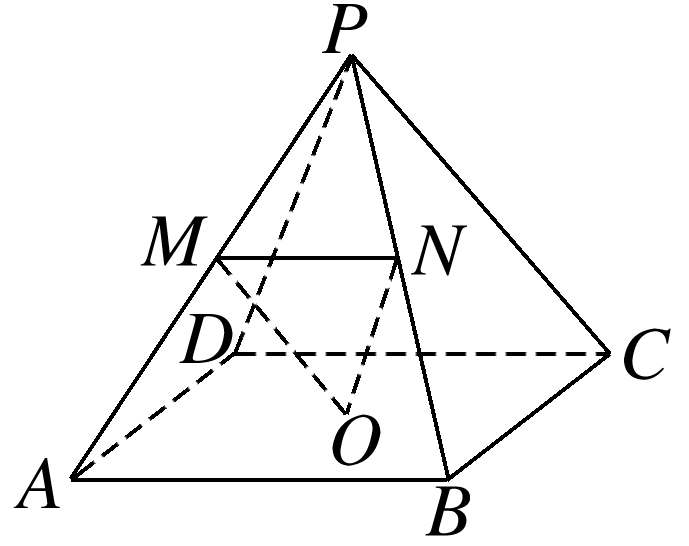
连接AC(图略),易得PC∥OM,又OM⊂平面OMN,PC⊄平面OMN,
所以PC∥平面OMN,故A正确;同理PD∥ON,又ON⊂平面OMN,PD⊄平面OMN,
所以PD∥平面OMN,又PC∩PD=P,PC,PD⊂平面PCD,所以平面PCD∥平面OMN,故B正确;由于四棱锥的棱长均相等,所以AB2+BC2=PA2+PC2=AC2,所以PC⊥PA,又PC∥OM,所以OM⊥PA,故C正确;由于M,N分别为侧棱PA,PB的中点,所以MN∥AB.又四边形ABCD为正方形,所以AB∥CD,所以直线PD与直线MN所成的角即为直线PD与直线CD所成的角,即∠PDC.又△PDC为等边三角形,所以∠PDC=60°,故D错误.
如图(1)所示,一个装了水的密封瓶子,其内部可以看成是由半径为1 cm和半径为3 cm的两个圆柱组成的简单几何体.当这个几何体如图(2)水平放置时,液面高度为20 cm;当这个几何体如图(3)水平放置时,液面高度为28 cm,则这个简单几何体的总高度为 cm.
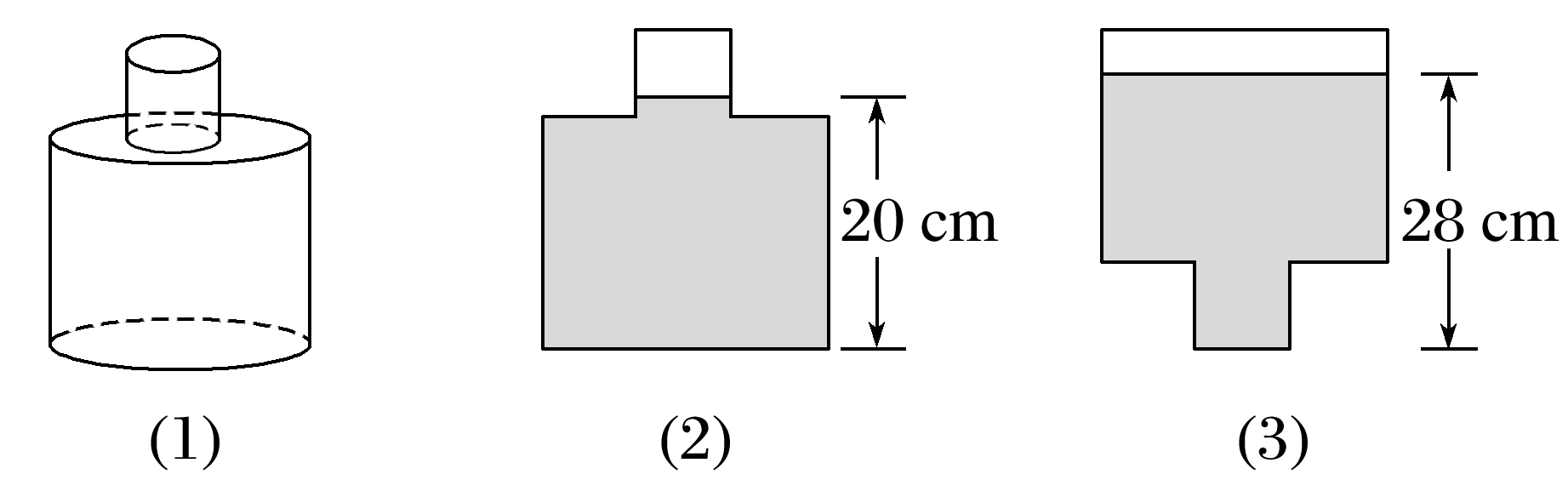
答案: 29
设上、下圆柱的半径分别是r cm,R cm,高分别是h cm,H cm.由水的体积不变得,πR2H+πr2(20-H)=πr2h+πR2(28-h),又r=1,R=3,故H+h=29.即这个简单几何体的总高度为29 cm.
有一个高为3π cm,底面半径为1 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 cm.
答案: 5π
把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD(如图所示),
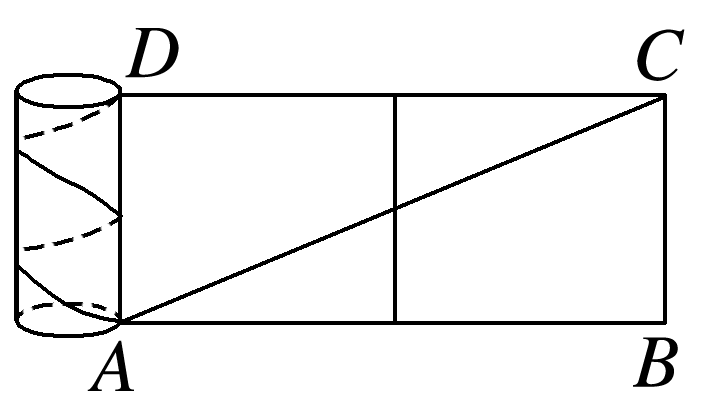
由题意知BC=3π cm,AB=4π cm,点A、点C分别是铁丝的起、止位置,故线段AC的长度即为铁丝的最短长度.AC==5π(cm),故铁丝的最短长度为5π cm.
在等腰梯形ABCD中,AB∥CD,AB=BC=3,CD=1,点O1,O2,E分别为CD,AB,BC的中点,以O1O2所在直线为旋转轴,将梯形旋转180°得到一旋转体,则直线AE与旋转体的上底面所成角的正切值为 .
答案:
由题意可知,所得到的旋转体是圆台,如图.
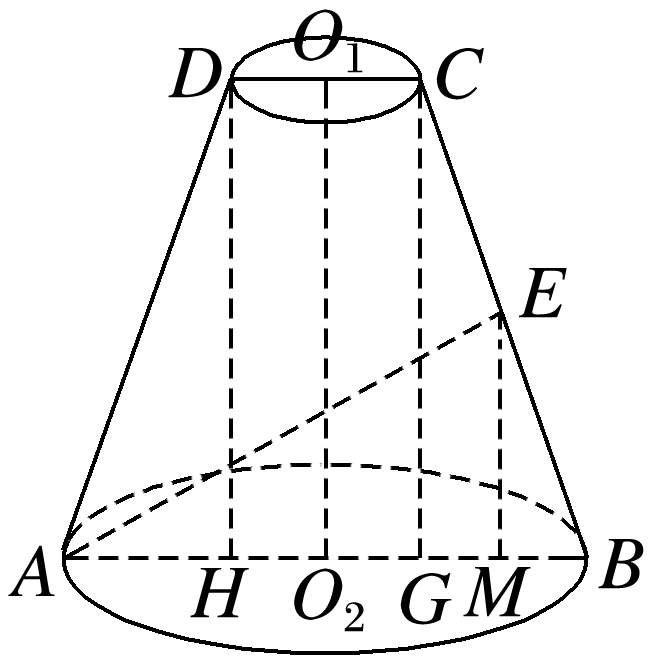
因为AB=3,CD=1,
所以圆台的上、下底面的半径分别满足r1=,r2=.
过点C,D分别作CG⊥AB于点G,DH⊥AB于点H,
则AH=HG=GB=1,所以DH==2,易知圆台的上、下底面平行,
所以直线AE与圆台的上底面所成的角等于其与圆台的下底面所成的角.过点E作EM⊥AB于点M.易知∠MAE为直线AE与下底面所成的角即为所求的角.又AM=AB-MB=AB-BG=3-,EM=CG=DH=,
所以tan∠MAE=.
如图,已知三棱柱ABC-A1B1C1中,A1C与AC1交于点O,D为BC边上一点,D1为B1C1中点,且A1B∥平面ADC1.求证:
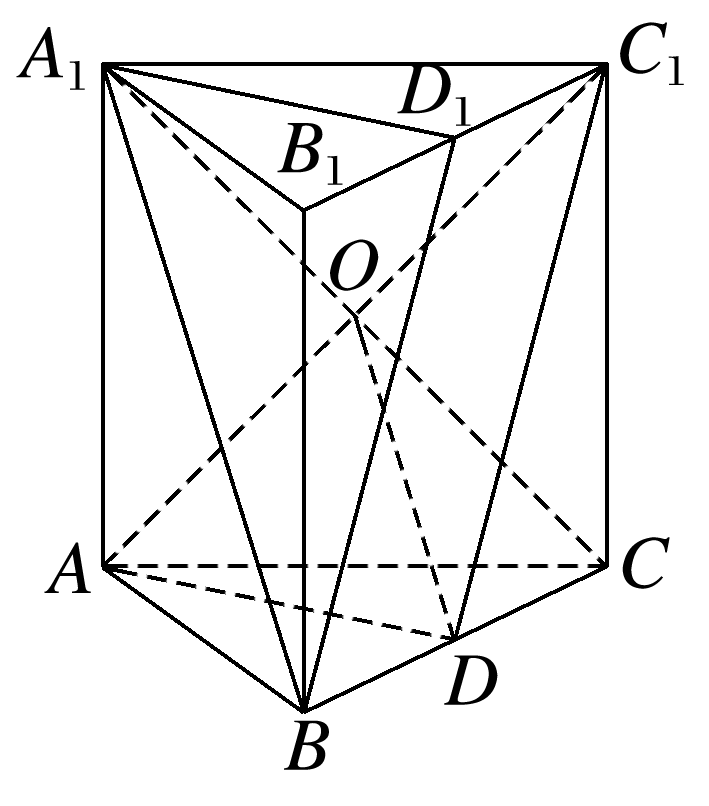
(1)A1B∥OD;
(2)平面A1BD1∥平面ADC1.
答案: 证明 (1)由题意,因为A1B∥平面ADC1, 且A1B⊂平面A1BC, 又因为平面ADC1∩平面A1BC=OD, 所以由线面平行的性质定理得A1B∥OD. (2)由(1)可知A1B∥OD, 又因为O点为A1C的中点, 所以D为BC的中点,即BD=BC, 因为D1为B1C1的中点, 即D1C1=B1C1, 又因为BC∥B1C1,BC=B1C1, 所以BD=D1C1,BD∥D1C1, 所以四边形BDC1D1为平行四边形, 所以BD1∥DC1, 又因为DC1⊂平面ADC1,BD1⊄平面ADC1, 所以BD1∥平面ADC1, 又A1B∥平面ADC1,A1B∩BD1=B, A1B⊂平面A1BD1,BD1⊂平面A1BD1, 所以平面A1BD1∥平面ADC1.
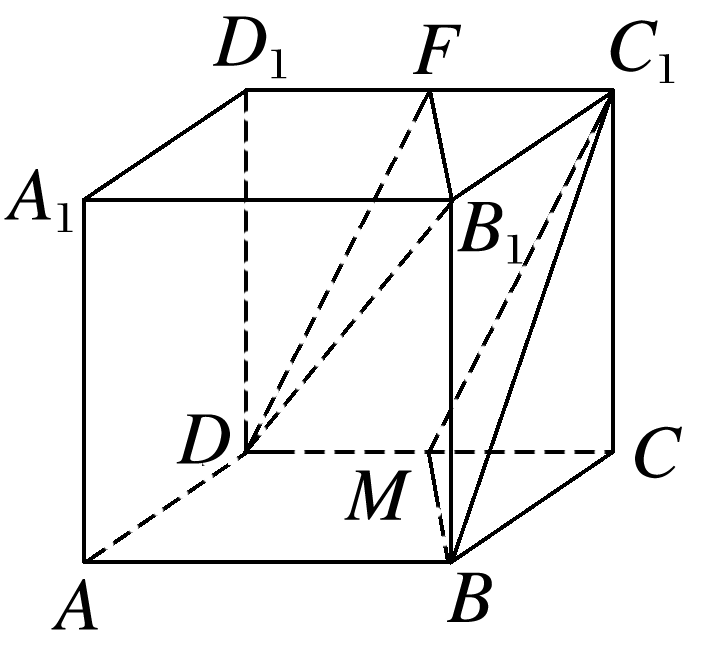
在长方体ABCD-A1B1C1D1中,AB=AA1=2AD=2,M是CD的中点.
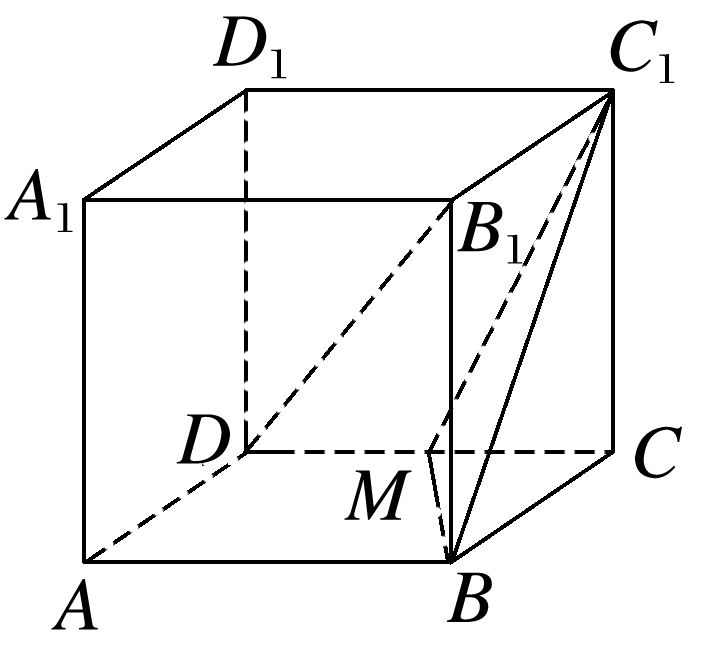
(1)证明:B1D∥平面BC1M;
(2)求异面直线B1D与MC1所成角的余弦值.
答案: (1)证明 连接B1C交BC1于点E, 则点E为BC1的中点,连接EM,所以EM∥B1D, 因为EM⊂平面BC1M, B1D⊄平面BC1M, 所以B1D∥平面BC1M. (2)解 取C1D1的中点F,连接DF,B1F, 则FC1=DM,FC1∥DM, 所以四边形FC1MD为平行四边形,可得C1M∥FD, 所以直线B1D与FD所成角∠FDB1或其补角即为异面直线B1D与MC1所成角, DF=, B1F=, DB1==3, 在△DB1F中由余弦定理得 cos∠FDB1=, 所以异面直线B1D与MC1所成角的余弦值为.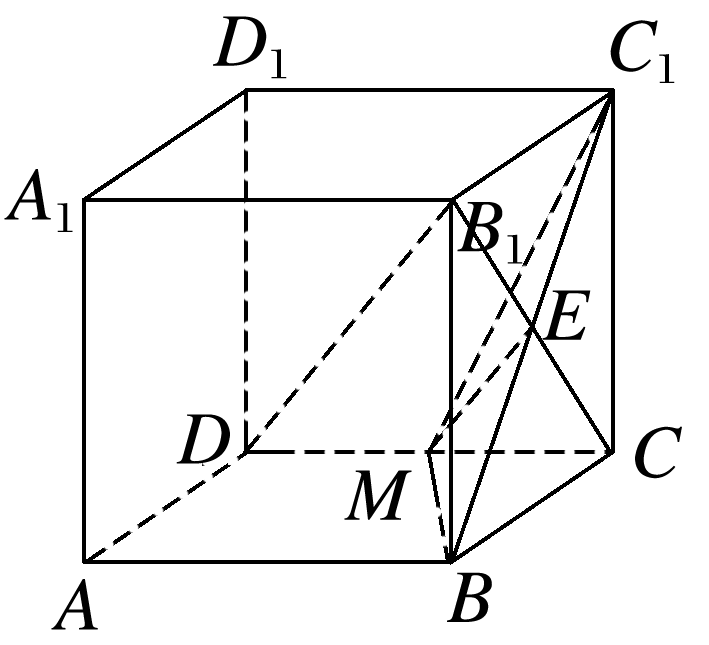
如图①,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图②中△A1BE的位置,得到四棱锥A1-BCDE.
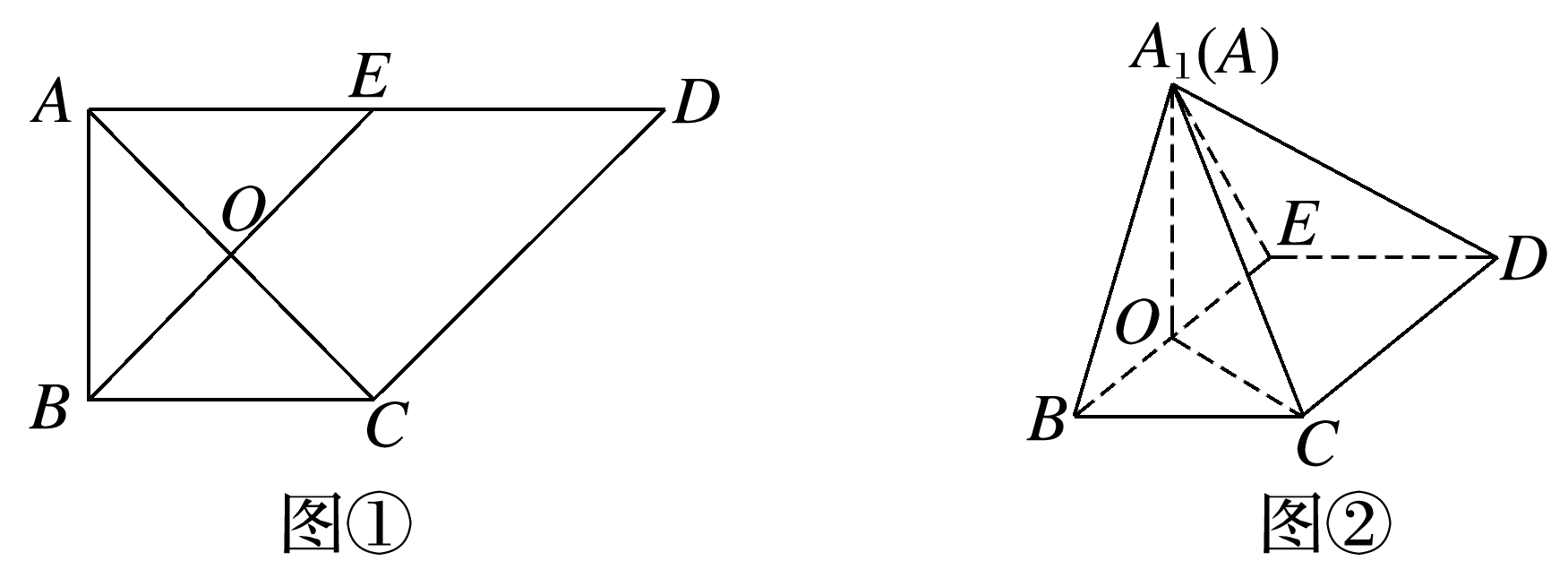
(1)求证:CD⊥平面A1OC;
(2)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36,求a的值.
答案: (1)证明 在图①中,因为AB=BC=AD=a, E是AD的中点,∠BAD=, 所以BE⊥AC. 即在图②中,BE⊥A1O,BE⊥OC, 又A1O∩OC=O,A1O,OC⊂平面A1OC, 从而BE⊥平面A1OC. 因为在图①中,BC 所以四边形BCDE为平行四边形, 所以在图②中,CD∥BE, 所以CD⊥平面A1OC. (2)解 由已知,平面A1BE⊥平面BCDE, 且平面A1BE∩平面BCDE=BE, 又由(1)可得A1O⊥BE, A1O⊂平面A1BE, 所以A1O⊥平面BCDE. 即A1O是四棱锥A1-BCDE的高. 由图①知,A1O=AB=a, 平行四边形BCDE的面积S=BC·AB=a2, 从而四棱锥A1-BCDE的体积为 V=S·A1O=×a2×a=a3. 由a3=36,得a=6.![]() AD
AD![]() ED,
ED,
在三棱柱ABC-A1B1C1中,底面△ABC是等腰三角形,且∠ABC=90°,侧面AA1B1B是菱形,∠A1AB=60°,平面AA1B1B⊥平面ABC,点M是AA1的中点.
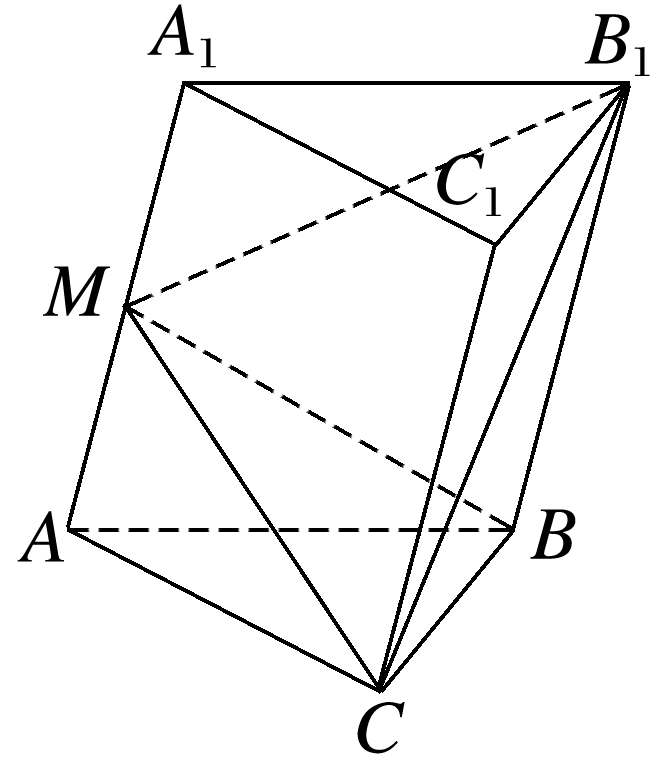
(1)求证:BB1⊥CM;
(2)求直线BM与平面CMB1所成角的正弦值.
答案: (1)证明 在Rt△ABC中,∠ABC=90°,即BC⊥AB, ∵平面ABC⊥平面AA1B1B,平面ABC∩平面AA1B1B=AB,BC⊂平面ABC, ∴BC⊥平面AA1B1B, ∵BB1⊂平面AA1B1B,∴BC⊥BB1. 在菱形AA1B1B中,∠A1AB=60°,连接A1B(图略), 则△A1AB是等边三角形, ∵点M是AA1的中点,∴AA1⊥BM. 又AA1∥BB1,∴BB1⊥BM, 又BM∩BC=B,BM,BC⊂平面BMC, ∴BB1⊥平面BMC,又CM⊂平面BMC, ∴BB1⊥CM. (2)解 如图,作BG⊥MB1于点G,连接CG. 由(1)知BC⊥平面AA1B1B, 又MB1⊂平面AA1B1B, ∴BC⊥MB1, 又BG⊥MB1,且BC∩BG=B, BC,BG⊂平面BCG,∴MB1⊥平面BCG. ∵MB1⊂平面CMB1, ∴平面CMB1⊥平面BCG,作BH⊥CG于点H,则BH⊥平面CMB1,连接MH, 则∠BMH即为直线BM与平面CMB1所成的角. 设AB=BC=2,则BB1=2,BM=, 在Rt△MBB1中,MB1=, 则BG=. 在Rt△CBG中,CG=, 则BH=, ∴sin∠BMH=, 即直线BM与平面CMB1所成角的正弦值为.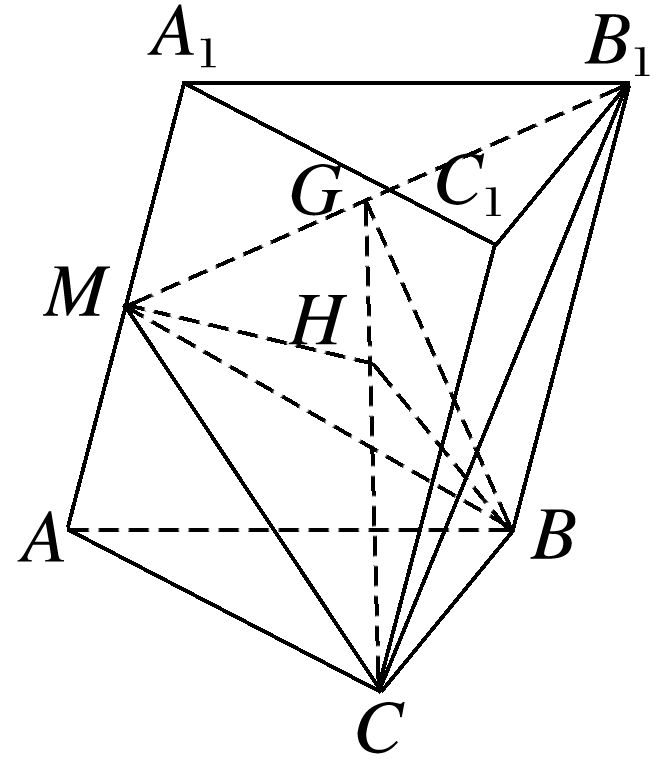
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,PD的中点为F.
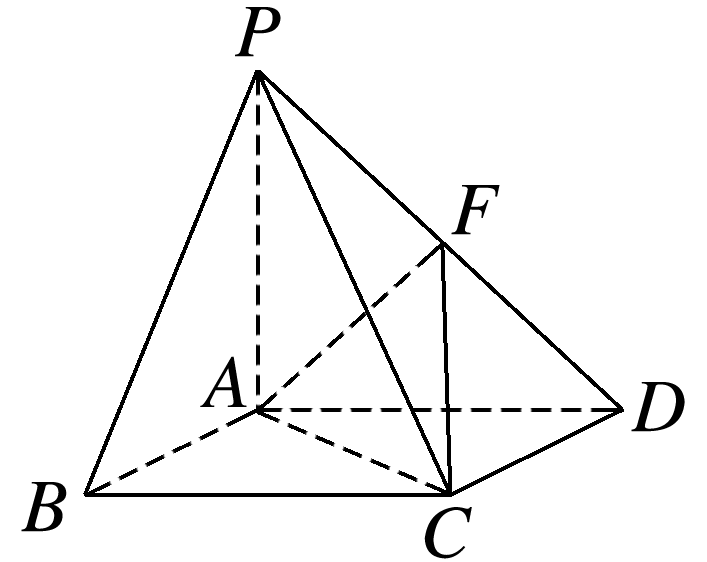
(1)在线段AB上是否存在一点G,使得AF∥平面PCG?若存在,指出点G在AB上的位置并给以证明;若不存在,请说明理由;
(2)请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC;②FC与平面ABCD所成的角为;
③∠ABC=.若 ,求二面角F-AC-D的余弦值.
注:如果选择多个条件分别解答,则按第一个解答计分
答案: 解 (1)在线段AB上存在中点G, 使得AF∥平面PCG.证明如下: 如图所示,连接PG,CG,设PC的中点为H,连接FH,GH, ∵FH∥CD,FH=CD, AG∥CD,AG=CD, ∴FH∥AG,FH=AG, ∴四边形AGHF为平行四边形,则AF∥GH. 又GH⊂平面PCG,AF⊄平面PCG, ∴AF∥平面PCG. (2)若选择条件①. 如图①,过点F作FM⊥AD于点M,过点M作MO⊥AC于点O,连接FO. ∵F为PD的中点,PA⊥平面ABCD, ∴FM∥PA,且FM⊥平面ABCD,又AC⊂平面ABCD,∴FM⊥AC. 又AC⊥MO,FM∩MO=M,FM,MO⊂平面FMO,∴AC⊥平面FMO,又FO⊂平面FMO, ∴AC⊥FO, ∴∠FOM为二面角F-AC-D的平面角. ∵AB⊥BC,四边形ABCD为正方形, ∴∠CAD=,∴MO=AMsin . 又FM=PA=1. ∴cos∠FOM=, 即二面角F-AC-D的余弦值为. 若选择条件②. 与选择条件①一样作相同的辅助线, 如图②,连接MC. ∵FC与平面ABCD所成的角为,∴∠FCM=, ∴MC=. ∴MC2+MD2=CD2,∴CM⊥AD. ∴在Rt△AMC中, MO=. ∴cos∠FOM=. 若选择条件③. 与选择条件①一样作相同的辅助线. ∵∠ABC=,∴∠DAC=, ∴MO=AMsin. ∴cos∠FOM=.