一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )
- A: 平行或异面
- B: 相交或异面
- C: 异面
- D: 相交
可以借助长方体来判断.如图,
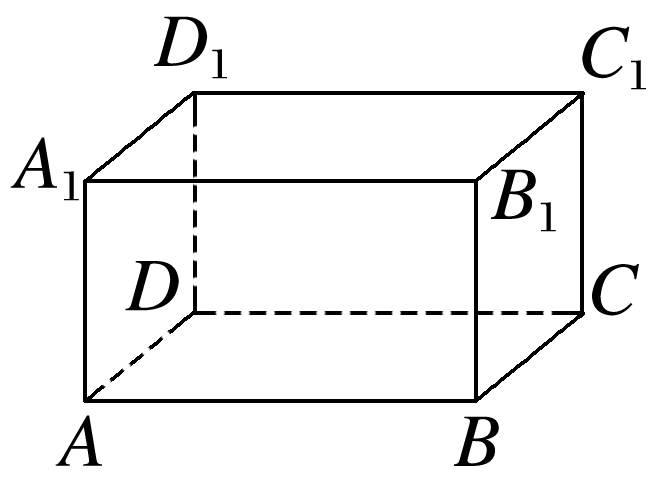
在长方体ABCD-A1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1,AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线,故选B.
一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )
可以借助长方体来判断.如图,

在长方体ABCD-A1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1,AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线,故选B.
过平面外两点作该平面的平行平面,可以作( )
平面外两点的连线与已知平面的位置关系有两种情况:
①直线与平面相交,可以作0个平行平面;
②直线与平面平行,可以作1个平行平面.
(课本P131练习T1(2))设直线a,b分别是长方体的相邻两个面的对角线所在的直线,则a与b( )
如图,长方体AC'中,
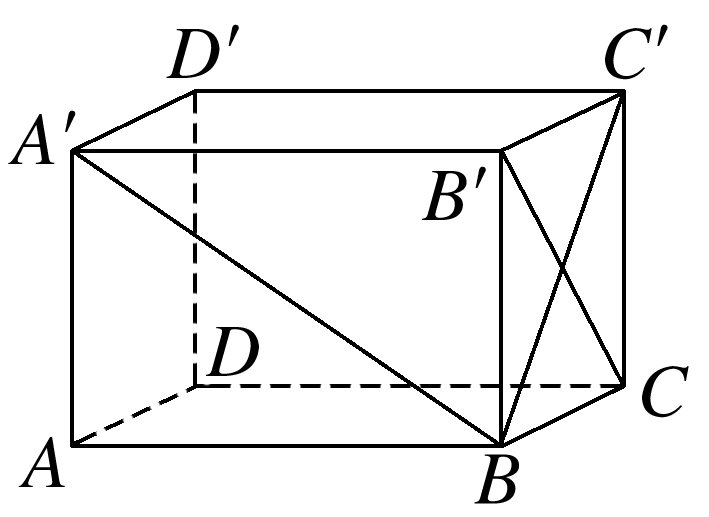
当A'B所在直线为a,BC'所在直线为b时,a与b相交;当A'B所在直线为a,B'C所在直线为b时,a与b异面,
∴长方体相邻两个面的对角线所在直线相交或异面.
(课本P132习题8.4T2(2))若直线a不平行于平面α,且a⊄α,则下列结论成立的是( )
∵直线a不平行于平面α,且a⊄α,
∴直线a与平面α相交,
∴α内的直线与a异面或相交,故A与D不成立;
α内不存在与a平行的直线,故B成立,C不成立.
如图,在三棱柱ABC-A1B1C1中,底面△A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是( )
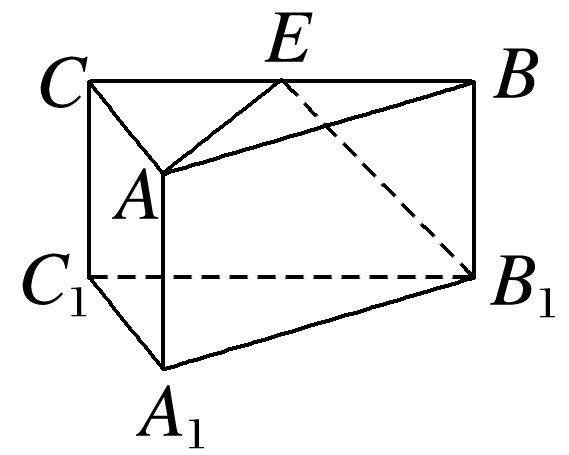
由于CC1与B1E都在平面C1B1BC内,故CC1与B1E是共面的;由异面直线的定义知C1C与AE是异面直线,AE与B1C1是异面直线,AE与B1B是异面直线.
平面α外的一条直线a与平面α内的一条直线b不平行,则 ( )
由题意,知a与α可能平行也可能相交.若a∥α,b⊂α,则a与b异面;若a与α相交,b⊂α,则a与b相交或异面,由此可知A,B,C均不正确.
下列说法正确的是( )
对于选项A,该直线可能在另一个平面内,A不正确;对于B,若两个平面α∥β,a⊂α,则a与β无公共点,即a∥β,B正确;对于C,若两个平面α∥β,a⊂α,b⊂β,则a与b无公共点,所以a与b一定不相交,C正确;对于D,若两个平面α∩β=b,a⊂α,则a与β可能相交,也可能平行,D正确.
如图,若G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有( )
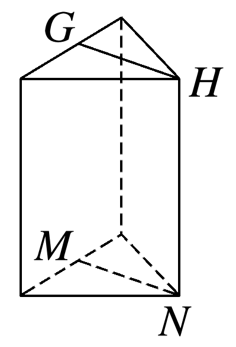
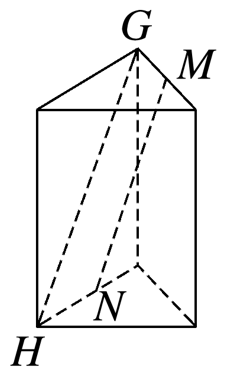
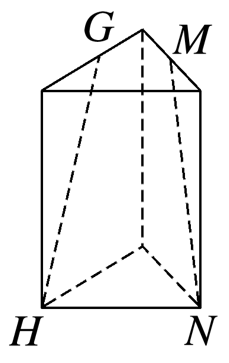
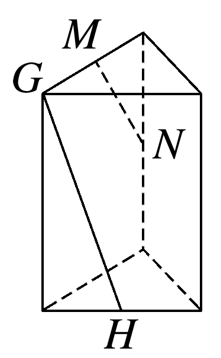
A中,GH∥MN;
C中,GM∥HN,且GM≠HN,
故GH,MN必相交;BD符合题意.
下列命题中是真命题的是( )
A中,直线a也可能与平面α相交,故A是假命题;B中,直线l与平面α相交时,l上也有无数个点不在平面α内,故B是假命题;C中,当l∥α时,l与α没有公共点,所以l与α内任何一条直线都没有公共点,故C是真命题;D中,长方体ABCD-A1B1C1D1中,A1C1与B1D1都与平面ABCD平行,且A1C1与B1D1相交,故D是真命题.
若点A∈α,B∉α,C∉α,则平面ABC与平面α的位置关系是 .
答案: 相交
∵点A∈α,B∉α,C∉α,
∴平面ABC与平面α有公共点,且不重合,
∴平面ABC与平面α的位置关系是相交.
如图是正方体的平面展开图,则在这个正方体中,CN,BM所在直线的位置关系为 .
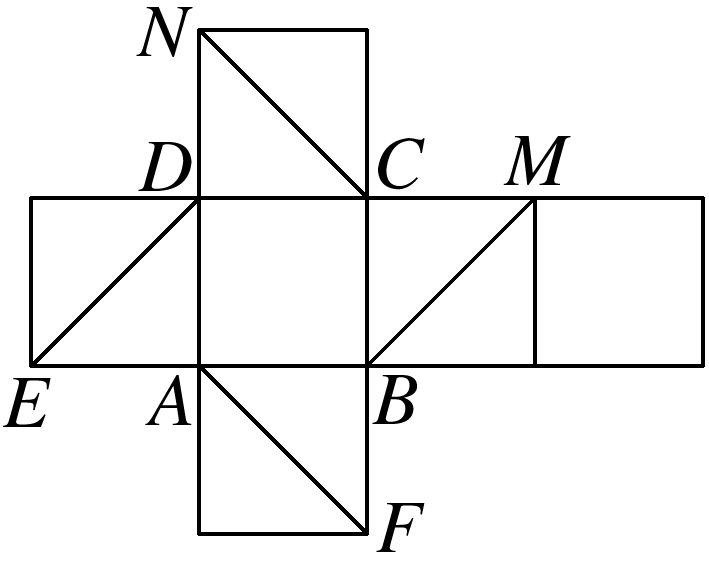
答案: 异面
将展开图还原后的图形如图所示,
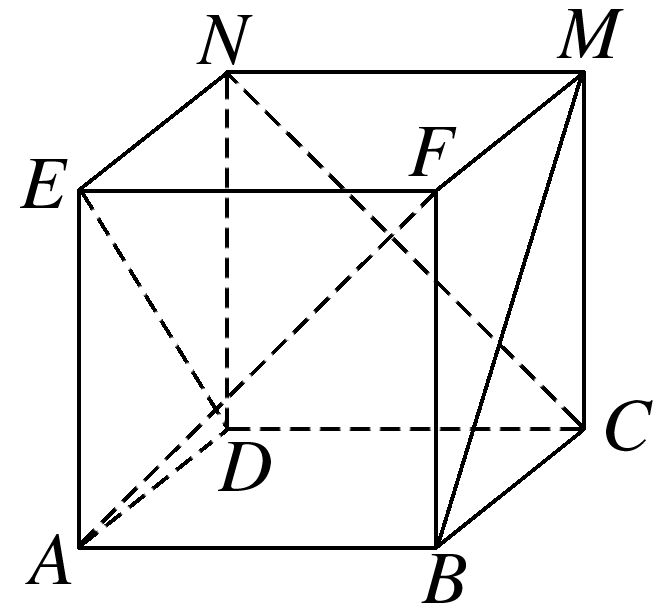
可知CN,BM所在直线异面.
若直线l上有两点到平面α的距离相等,则直线l与平面α的关系是 .
答案: 平行或相交或l⊂α
当l∥α时,l上有两点到平面α的距离相等;
当l与α相交时,l上有两点到平面α的距离相等;
当l⊂α时,l上有两点到平面α的距离相等,
故l∥α或l与α相交或l⊂α.
如图,在正方体ABCD-A1B1C1D1中,判断下列位置关系:
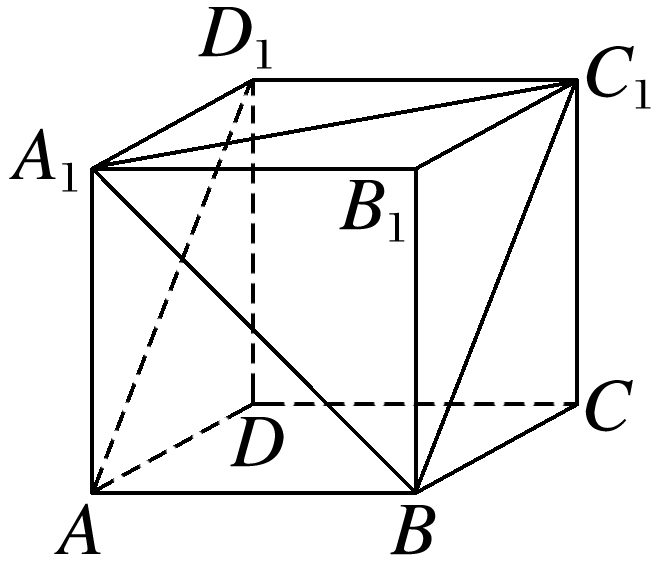
(1)AD1所在直线与平面BCC1的位置关系是 ;
(2)平面A1BC1与平面ABCD的位置关系是 .
答案: (1)平行 (2)相交
(1)AD1所在的直线与平面BCC1没有公共点,所以平行.
(2)平面A1BC1与平面ABCD有公共点B,故相交.
如图所示,在长方体ABCD-A1B1C1D1中,直线B1D1与长方体的六个面之间的位置关系如何?
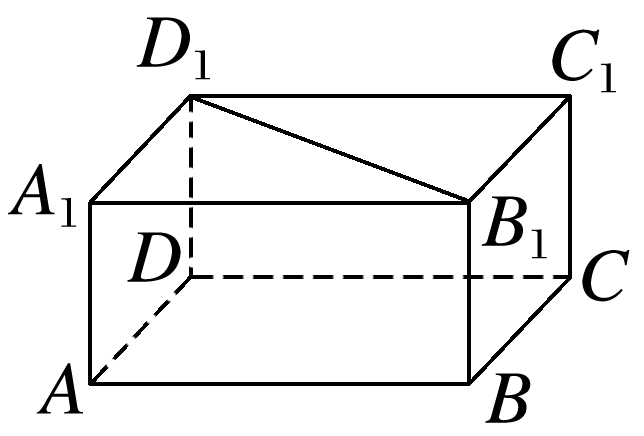
答案: 解 B1D1在平面A1B1C1D1内, B1D1与平面BCC1B1, 平面ABB1A1,平面ADD1A1, 平面CDD1C1都相交, B1D1与平面ABCD平行.
如图,在三棱锥S-ABC中,E,F分别为AC,BC的中点,G为SC上靠近点C的三等分点,证明:平面EFG与平面SAB相交.
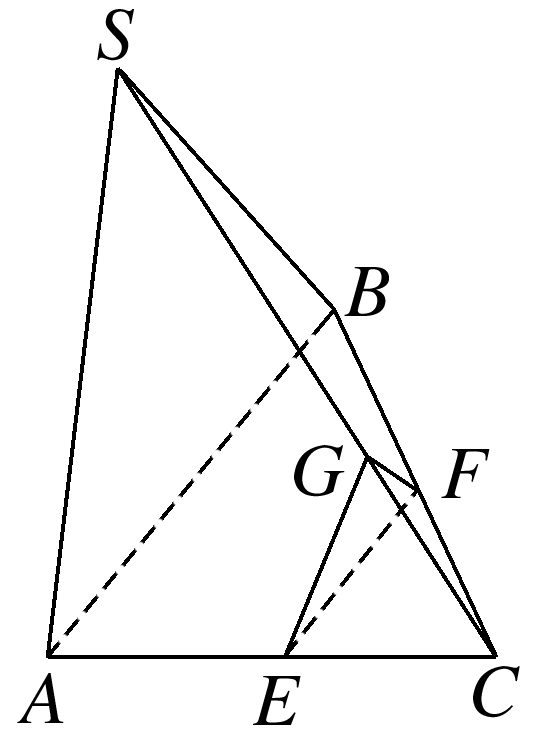
答案: 证明 因为E为AC的中点,G为SC上靠近点C的三等分点,所以EG与SA不平行,且EG,SA共面,则SA与EG所在直线必然相交于一点,设此点为M,则M∈SA,M∈EG,又SA⊂平面SAB,EG⊂平面EFG,则M∈平面SAB,M∈平面EFG,故平面EFG与平面SAB相交.
如图,平面α,β,γ满足α∥β,α∩γ=a,β∩γ=b,判断a与b,a与β的位置关系并证明你的结论.
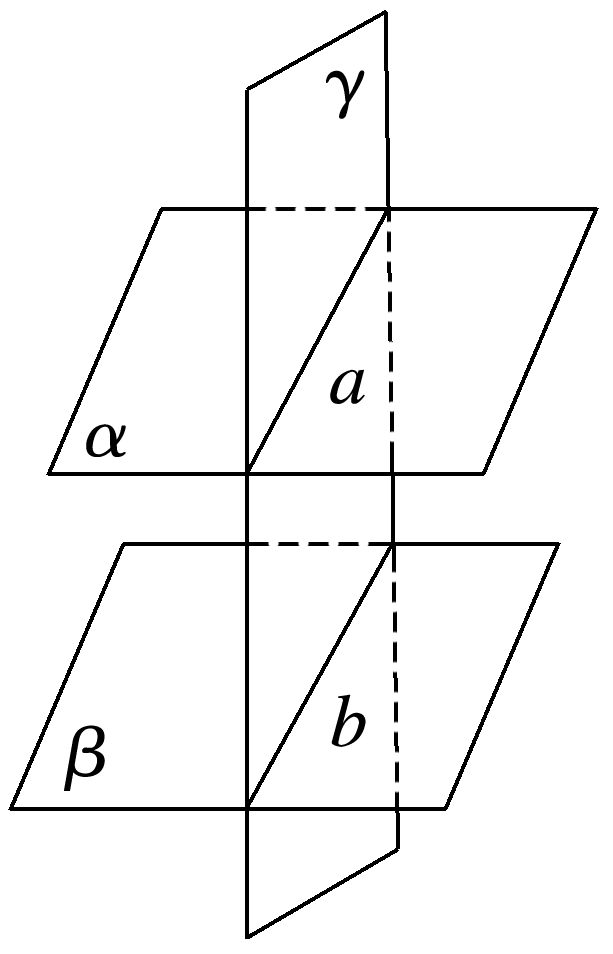
答案: 解 a∥b,a∥β.证明如下: 由α∩γ=a知a⊂α且a⊂γ, 由β∩γ=b知b⊂β且b⊂γ. ∵α∥β,a⊂α,b⊂β, ∴a,b无公共点. 又a⊂γ且b⊂γ,∴a∥b. ∵α∥β, ∴α与β无公共点. 又a⊂α, ∴a与β无公共点,∴a∥β.
在以下四个图中,直线a与直线b平行的位置关系只能是( )
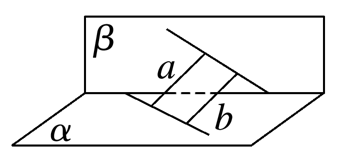
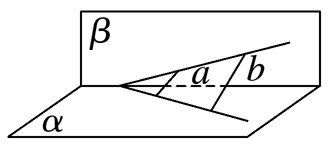
选项A中,平面α,β内的两直线异面,则a与b异面;
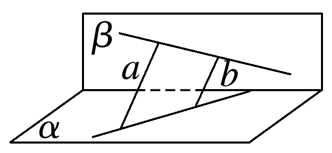
选项B中,平面α,β内的两直线异面,则a与b异面;
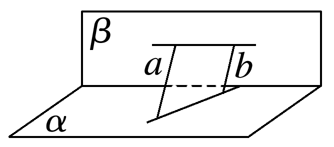
选项C中,平面α,β内的两直线异面,则a与b异面;
选项D中,平面α,β内的两直线相交,两相交直线可以确定一个平面,
则a与b相交或平行,由图可知,a与b平行.
如图,若P是△ABC所在平面外一点,PA≠PB,PN⊥AB,N为垂足,M为AB的中点,求证:PN与MC为异面直线.
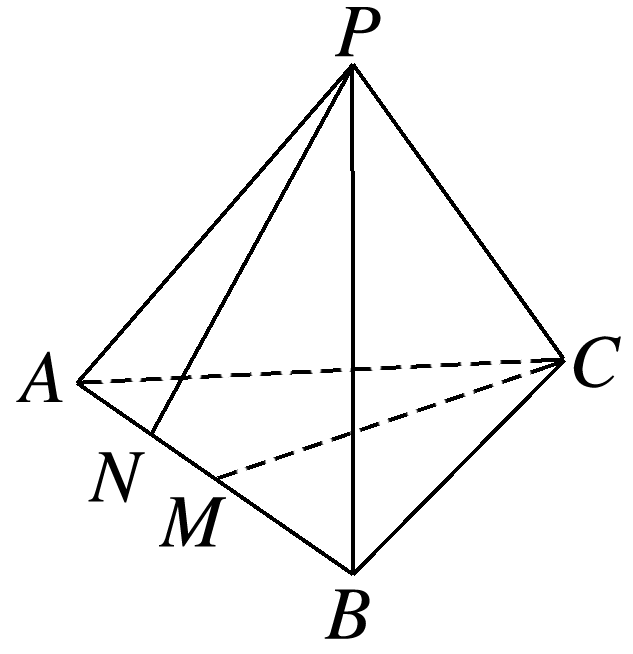
答案: 证明 方法一 因为PA≠PB,PN⊥AB,N为垂足,M是AB的中点,所以点N与点M不重合. 因为N∈平面ABC,P∉平面ABC,CM⊂平面ABC,N∉CM,所以PN与MC为异面直线. 方法二 假设PN与MC不是异面直线,则存在一个平面α,使得PN⊂α,MC⊂α, 于是P∈α,C∈α,N∈α,M∈α. 因为PA≠PB,PN⊥AB,N为垂足,M是AB的中点,所以点M与点N不重合. 因为M∈α,N∈α,所以MN⊂α. 因为A∈MN,B∈MN,所以A∈α,B∈α,即A,B,C,P四点均在平面α内,这与点P在平面ABC外矛盾.所以假设不成立.故PN与MC为异面直线.