如图所示,质量关系为m1>m2>m3的三个小球分别沿三条不同的轨道1、2、3由离地高h的A点滑到同一水平面上,轨道1、3是光滑的,轨道2是粗糙的,重力对小球做的功分别为W1、W2、W3,则下列判断正确的是( )
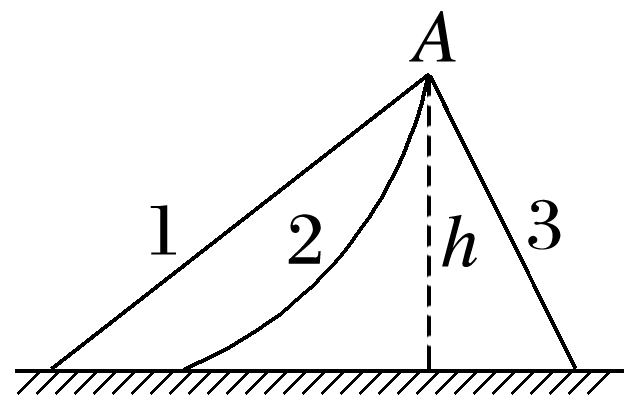
- A: W1>W2=W3
- B: W1=W3>W2
- C: W1=W2=W3
- D: W1>W2>W3
重力做功W=mgh,h相等,由于m1>m2>m3,所以W1>W2>W3,故D正确。
如图所示,质量关系为m1>m2>m3的三个小球分别沿三条不同的轨道1、2、3由离地高h的A点滑到同一水平面上,轨道1、3是光滑的,轨道2是粗糙的,重力对小球做的功分别为W1、W2、W3,则下列判断正确的是( )

重力做功W=mgh,h相等,由于m1>m2>m3,所以W1>W2>W3,故D正确。
某游客领着孩子游泰山时,孩子不小心将手中质量为m的皮球滑落,球从A点滚到了山脚下的B点,高度标记如图所示,重力加速度为g,则下列说法正确的是( )
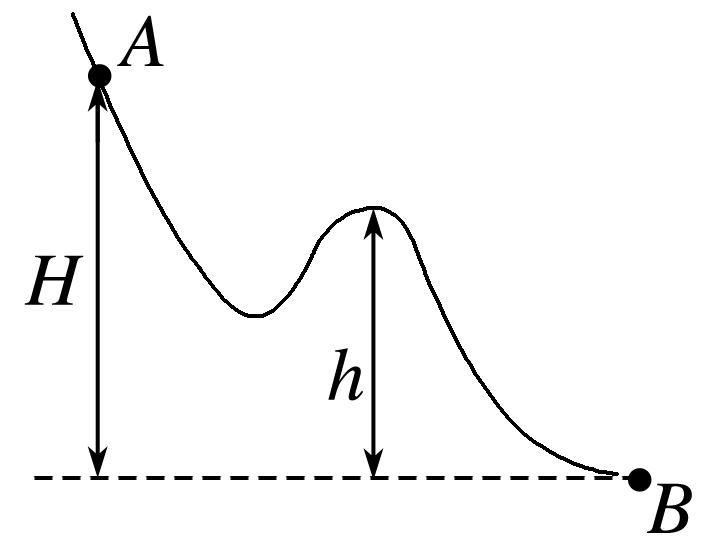
重力做功与物体的运动路径无关,只与物体初、末位置的高度差有关。从A到B的高度差是H,故从A到B重力做的功是mgH,选项D正确。
选定了参考平面之后,一个物体的重力势能是-50 J,这里的“-”表示( )
重力势能是标量,A错误;物体的重力势能是-50 J,表明物体位于选定的参考平面之下,比它在参考平面时的重力势能小50 J,B正确;从参考平面移到该位置,重力对物体做功50 J,而从该位置移到参考平面,物体克服重力做功50 J,C、D错误。
(2024·台州市高一期中)如图所示,一质量为m的游客乘坐摩天轮观光。假设该游客随摩天轮在竖直平面内做半径为R的圆周运动,重力加速度为g。在游客从最低点转过90°的过程中,其重力势能的增加量为( )

在游客从最低点转过90°的过程中,游客上升的高度为R,游客重力势能的增加量为ΔEp=mgR,故选A。
(2024·宁波市高一期中)如图所示,利用矿坑所建造的上海深坑酒店,设有地平面上3层约15米,地平面以下16层,其中2层在坑底湖水的水下,深度有10米。若建筑物包括水面下的总高度为75米,则一质量为60 kg的人立于地平面下20米的客房中,其重力势能相对于地平面是多少?若改以湖水水面为零势能面,其重力势能是多少?(重力加速度g=10 m/s2)( )

一质量为60 kg的人立于地平面下20米的客房中,其重力势能相对于地平面为Ep=-mgh=-60×10×20 J=-12 000 J,若改以湖水水面为零势能面,其重力势能为Ep′=mgh′=60×10×(75-15-20-10) J=18 000 J,故选B。
广西壮族“三月三”是壮族人民的传统节日,该节日民族活动很丰富,其中抛绣球是男女青年最喜欢的项目。假设某一青年女子在楼上将绣球水平抛出,抛出点离地4.5 m,绣球质量0.6 kg,在离地2.0 m处被一男青年抢到。重力加速度取10 m/s2,在绣球被抛出至被抢到的过程中,下列说法正确的是( )
重力做功为WG=mgΔh=0.6×10×(4.5-2.0)=15 J,A正确;重力做正功,重力势能减小,故重力势能减少了15 J,B错误;若以抛出点为参考平面,绣球被抢到时的重力势能Ep=-mg(h-h1)=-0.6×10×(4.5-2) J=-15 J,C错误;重力势能的变化量与重力做功对应,与参考平面的选取无关,D错误。
关于弹簧的弹性势能,下列说法中正确的是( )
当弹簧始终处于压缩状态时,弹簧变长后弹性势能将减小,弹簧变短后弹性势能将增大,故A、B错误;弹簧的弹性势能与劲度系数和形变量有关,弹簧劲度系数k相同,弹簧拉伸时和压缩时形变量相等的情况下,两者弹性势能相等,故C错误;弹簧的弹性势能与劲度系数和形变量有关,在弹簧被拉伸的长度相同时,劲度系数k越大的弹簧,它的弹性势能越大,故D正确。
如图所示,轻弹簧下端系一重物,O点为其平衡位置(即重力和弹簧弹力大小相等的位置),今用手向下拉重物,第一次把它直接拉到A点,弹力做功为W1,第二次把它由O点拉到B点后再让其回到A点,弹力做功为W2,则这两次弹力做功的关系为( )
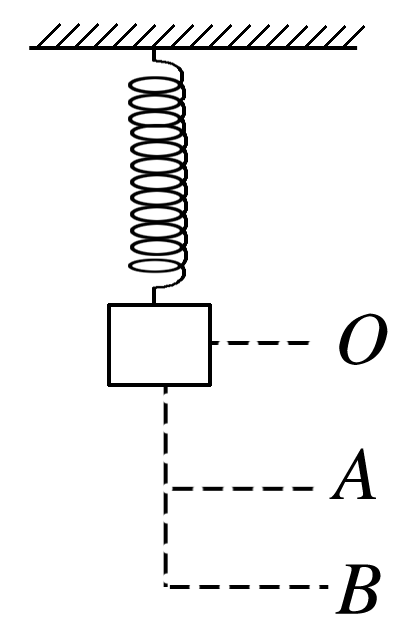
弹力做功与路径无关,只与初、末位置有关,两次初、末位置相同,故W1=W2,故D正确。
如图所示,在光滑水平面上有一物体与水平轻质弹簧相连,弹簧的另一端固定在墙上,在水平力F的作用下物体处于静止状态,当撤去力F后,物体将向右运动。在物体向右运动的过程中,下列说法正确的是( )
![]()
由于在水平力F的作用下物体处于静止状态,此时弹簧处于压缩状态,撤去力F后,在物体向右运动的过程中,弹簧先恢复到原长,然后继续伸长,弹簧的弹力对物体先做正功后做负功,所以弹簧的弹性势能先减小后增大,故D正确。
一根粗细均匀的长直铁棒重力为600 N,平放在水平地面上。现将其一端从地面抬高0.50 m,而另一端仍在地面上,则铁棒( )
由几何关系可知铁棒的重心上升的高度为h=×0.5 m=0.25 m,克服重力做功W克G=Gh=600×0.25 J=150 J,故铁棒重力势能增加150 J,故选A。
如图所示,一质量为m、长度为l的均匀柔软细绳PQ竖直悬挂。用外力将绳的下端Q缓慢地竖直向上拉起至M点,M点与绳的上端P相距l。重力加速度大小为g。在此过程中,绳的重力势能增加( )
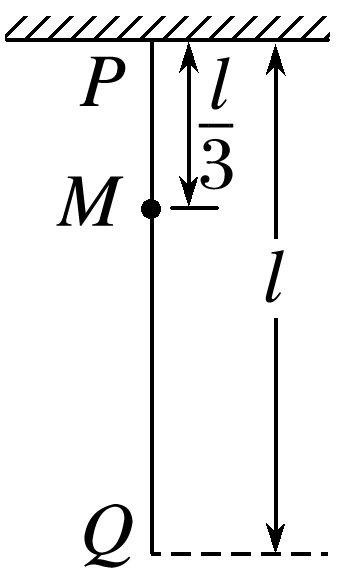
由题意可知,PM段细绳的重力势能不变,MQ段细绳的重心升高了,则重力势能增加ΔEp=mg·=mgl,故选项A正确,B、C、D错误。
在离地面80 m处无初速度释放一小球,小球质量为m=200 g(不计空气阻力,g取10 m/s2),取释放点所在水平面为参考平面,求:
(1)在第2 s末小球的重力势能;
(2)在第3 s内重力所做的功和重力势能的变化量。
答案: (1)-40 J (2)50 J 减少50 J
(1)以释放点所在水平面为参考平面,在第2 s末小球所处的高度h=-gt2=-×10×22 m=-20 m
重力势能Ep=mgh=0.2×10×(-20) J=-40 J
(2)在第3 s末小球所处的高度h′=-gt′2=-×10×32 m=-45 m
第3 s内重力做功W=mg(h-h′)=0.2×10×(-20+45) J=50 J,
重力势能的变化量等于重力所做功的大小,故小球的重力势能减少50 J。
(多选)一轻质弹簧的弹力与弹簧形变量之间的关系如图甲所示。将该弹簧下端固定在水平地面上,一质量为1.8 kg的物体在外力作用下缓慢放在竖直弹簧的上端,待物体稳定后撤去外力,物体静止在弹簧上端,弹簧处在弹性限度内,如图乙所示,取重力加速度大小g=10 m/s2,则下列说法正确的是( )
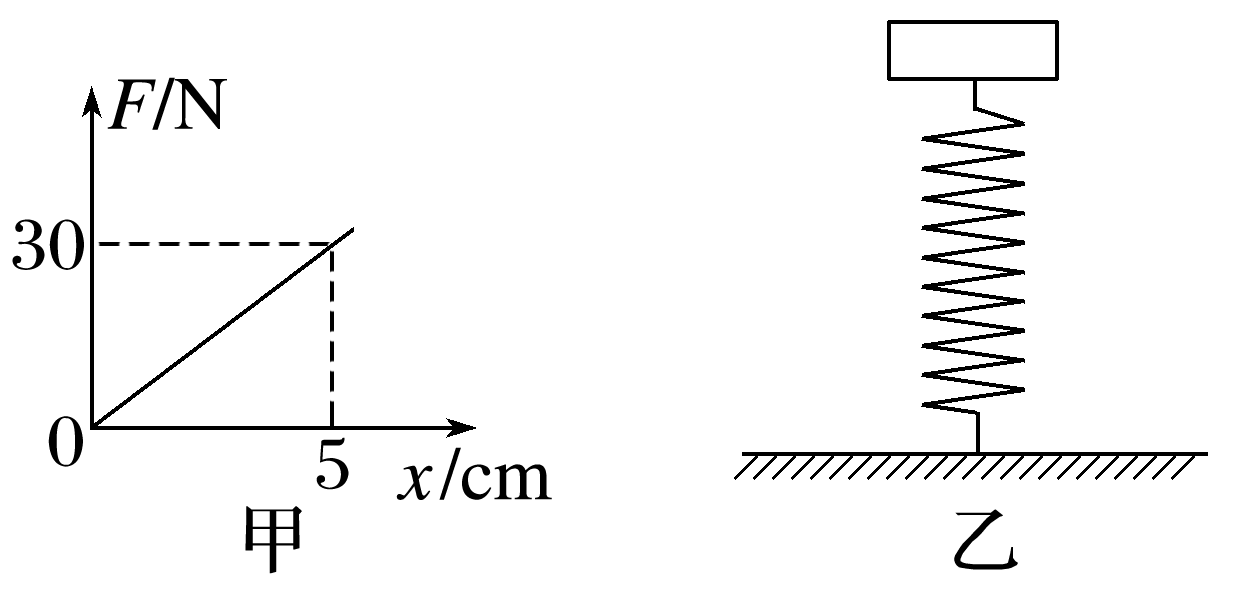
由题图甲知,弹簧的劲度系数k==600 N/m,弹簧的压缩量满足mg=kx,解得x=3 cm,A正确;弹簧的形变量越大,弹性势能越大,B错误;由题图甲知,缓慢压缩过程弹簧弹力对物体做功为W=-×18×0.03 J=-0.27 J,则物体静止时弹簧弹性势能为0.27 J,C错误,D正确。