第八章周练5(范围：§8.1~§8.3)

第1题 (单选题) 难度 - 基础题：

如图所示的几何体是数学奥林匹克竞赛的奖杯，该几何体由(　　)

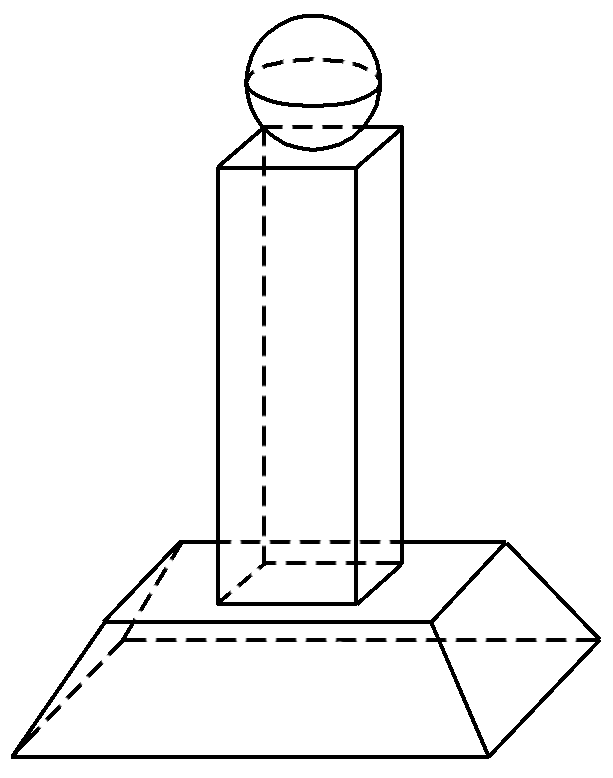
A: 一个球、一个四棱柱、一个圆台构成
B: 一个球、一个长方体、一个棱台构成
C: 一个球、一个四棱台、一个圆台构成
D: 一个球、一个五棱柱、一个棱台构成

解析:

由图可知，该几何体是由一个球、一个长方体、一个棱台构成.

第2题 (单选题) 难度 - 基础题：

下列关于圆柱的说法中不正确的是(　　)

A: 圆柱的所有母线长都相等
B: 用平行于圆柱底面的平面截圆柱，所得截面是与底面全等的圆面
C: 用一个平面截圆柱，所得截面始终是圆面
D: 一个矩形以其对边中点的连线为旋转轴，旋转180°所形成的几何体是圆柱

解析:

用一个不平行于圆柱底面的平面，如和轴平行的平面截圆柱，截面可以是矩形，故C错.

第3题 (单选题) 难度 - 基础题：

已知一个球的表面积是16π，则它的体积是(　　)

A: 64π
B: $\frac{64 π}{3}$
C: 32π
D: $\frac{32 π}{3}$

解析:

设球的半径为R，则由题意可知4πR²＝16π，解得R＝2.所以球的体积V＝ $\frac{4}{3}$ πR³＝ $\frac{32 π}{3}$ .

第4题 (单选题) 难度 - 基础题：

建盏是福建省南平市建阳区的特产，是中国国家地理标志产品，其多是口大底小，底部多为圈足且圈足较浅(如图所示)，因此可将建盏看作是圆台与圆柱拼接而成的几何体.现将某建盏的上半部分抽象成圆台O₁O₂，已知该圆台的上、下底面积分别为16π cm²和9π cm²(这里的上底面是指大的那个底面)，高超过1 cm，该圆台上、下底面圆周上的各个点均在球O的表面上，且球O的表面积为100π cm²，则该圆台的体积为(　　)

A: 80π cm³
B: $\frac{259 π}{3}$ cm³
C: $\frac{260 π}{3}$ cm³
D: 87π cm³

解析:

设球O的半径为R，上、下底面分别为圆O₁，O₂(这里上底面是指大的那个底面)，

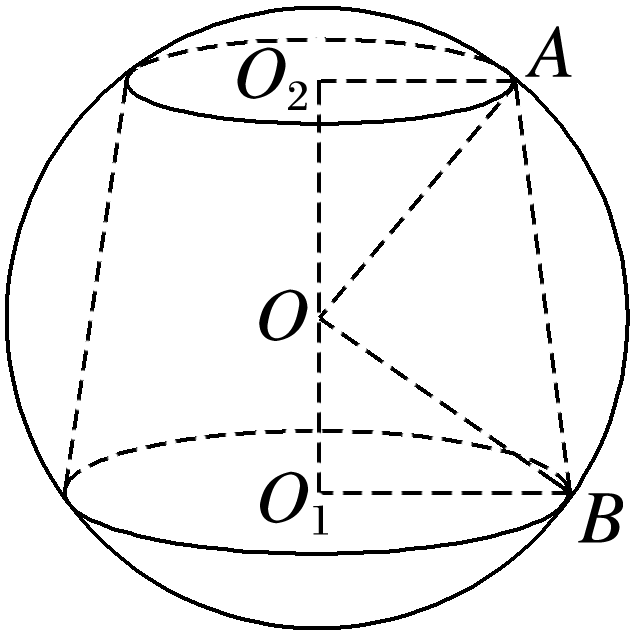
依题意，4πR²＝100π，解得R＝5，

因为O₂A²＝9＝3²，

则OO₂＝ $\sqrt{R^{2} - 3^{2}}$ ＝4(cm)，同理可得，OO₁＝3 cm，

因为圆台的高超过1 cm，则该圆台的高为7 cm，

该圆台的体积为 $\frac{1}{3}$ ×(9π＋16π＋12π)×7＝ $\frac{259 π}{3}$ (cm³).

第5题 (单选题) 难度 - 基础题：

在如图所示的多面体ABCDD₁B₁C₁中，四边形ABCD、四边形BCC₁B₁、四边形CDD₁C₁都是边长为6的正方形，则此多面体的体积是(　　)

A: 72
B: 144
C: 180
D: 216

解析:

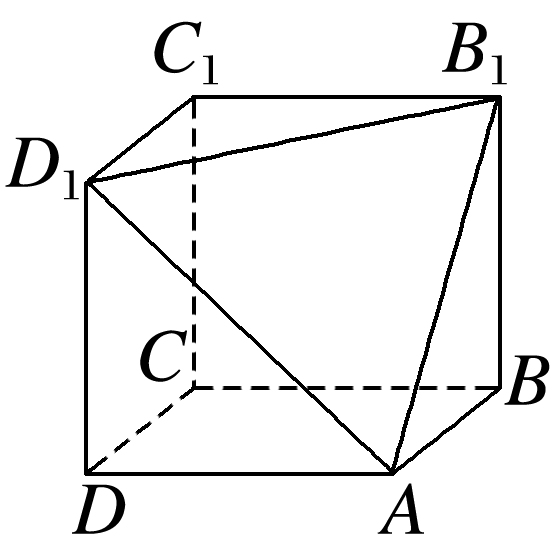
把该多面体补成一个正方体ABCD－A₁B₁C₁D₁，如图所示，

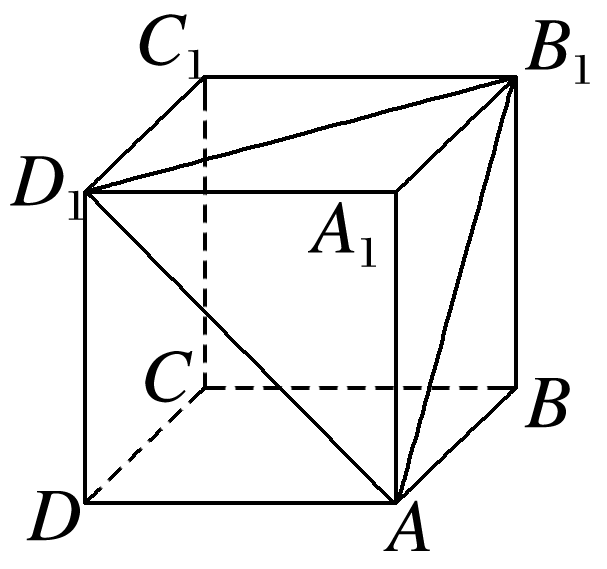
所求体积

V＝V_正方体－ $V_{三棱锥 A - A_{1} B_{1} D_{1}}$

＝6³－ $\frac{1}{3}$ × $\frac{1}{2}$ ×6×6×6＝180.

第6题 (单选题) 难度 - 基础题：

南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时，相应水面的面积为140.0 km²；水位为海拔157.5 m时，相应水面的面积为180.0 km².将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5 m上升到157.5 m时，增加的水量约为( $\sqrt{7}$ ≈2.65)(　　)

A: 1.0×10⁹ m³
B: 1.2×10⁹ m³
C: 1.4×10⁹ m³
D: 1.6×10⁹ m³

解析:

如图，由已知得该棱台的高为157.5－148.5＝9(m)，

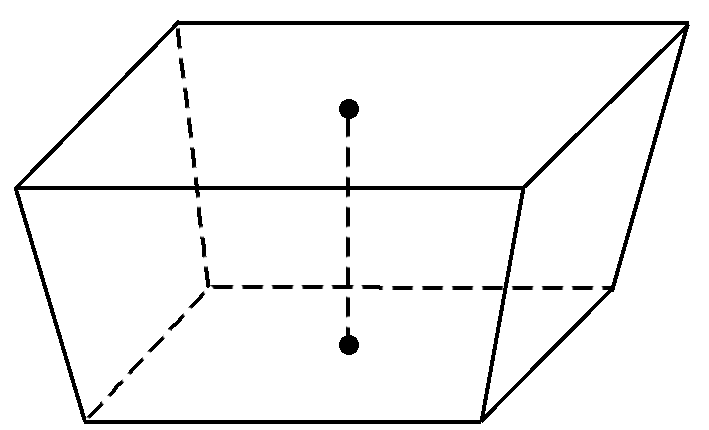
所以该棱台的体积V＝ $\frac{1}{3}$ ×9×(140＋ $\sqrt{140 \times 180}$ ＋180)×10⁶＝60×(16＋3 $\sqrt{7}$ )×10⁶≈60×(16＋3×2.65)×10⁶＝1.437×10⁹≈1.4×10⁹(m³).

第7题 (多选题) 难度 - 基础题：

下列说法中，正确的是(　　)

A: 棱柱中每一个面都不会是三角形
B: 各个侧面都是正方形的四棱柱不一定是正方体
C: 经过圆锥的两条母线的截面一定是一个等腰三角形
D: 用斜二测画法作水平放置的平面图形的直观图时，正方形的直观图是菱形

解析:

A选项，三棱柱的上底面和下底面是三角形，A错误；B选项，各个侧面都是正方形，若上、下底面是菱形，则这样的四棱柱不是正方体，B正确；C选项，圆锥的两条母线相等，故经过圆锥的两条母线的截面一定是一个等腰三角形，C正确；D选项，用斜二测画法作水平放置的平面图形的直观图时，如图所示，正方形的直观图不是菱形，D错误.

第8题 (多选题) 难度 - 基础题：

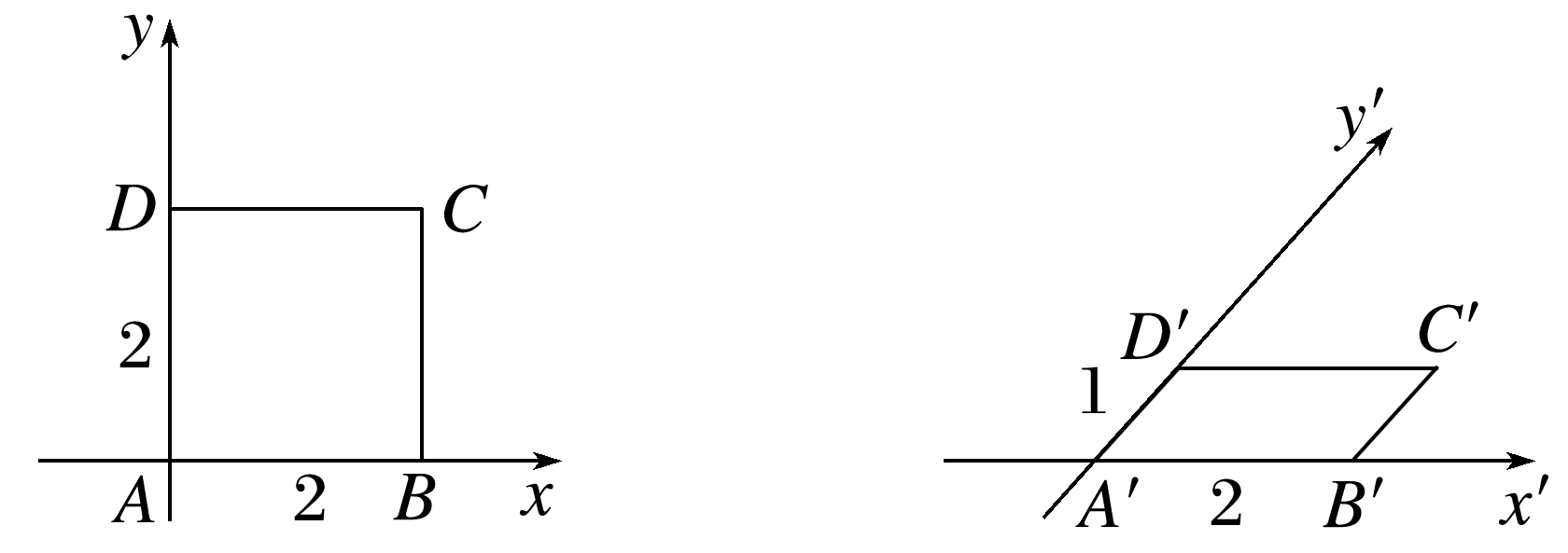
已知圆锥AO₁的底面圆O₁的半径与球O₂的半径相等，且圆锥AO₁的表面积与球O₂的表面积相等，则(　　)

A: 圆锥AO₁的底面圆O₁的直径与母线长之比为 $\frac{2}{3}$
B: 圆锥AO₁的高与母线长之比为 $\frac{2}{3}$
C: 圆锥AO₁的侧面积与底面积之比为3
D: 球O₂的体积与圆锥AO₁的体积之比为 $\sqrt{2}$

解析:

设圆锥AO₁的底面圆O₁的半径为R，

高为h，母线长为l，由圆锥AO₁的表面积与球O₂的表面积相等，得πRl＋πR²＝4πR²，解得l＝3R，因此圆锥AO₁的底面圆O₁的直径与母线长之比为 $\frac{2 R}{l} ＝ \frac{2}{3}$ ，A正确；

h＝ $\sqrt{l^{2} - R^{2}}$ ＝2 $\sqrt{2}$ R，因此圆锥AO₁的高与母线长之比为 $\frac{h}{l} ＝ \frac{2 \sqrt{2}}{3}$ ，B错误；圆锥AO₁的侧面积与底面积之比为 $\frac{π R l}{π R^{2}} ＝ \frac{l}{R}$ ＝3，C正确；球O₂的体积与圆锥AO₁的体积之比为 $\frac{\frac{4}{3} π R^{3}}{\frac{1}{3} π R^{2} \cdot 2 \sqrt{2} R} ＝ \sqrt{2}$ ，D正确.

第9题 (多选题) 难度 - 基础题：

已知一圆锥的母线长为2，底面半径为r，其侧面展开图是圆心角为 $\sqrt{3}$ π的扇形，A，B为底面圆的一条直径上的两个端点，则下列结论中正确的是(　　)

A: r＝ $\sqrt{3}$
B: 从A点经过圆锥的表面到达B点的最短距离为2 $\sqrt{3}$
C: 该圆锥的体积为π
D: 过该圆锥的顶点作圆锥的截面，则截面面积的最大值为 $\sqrt{3}$

解析:

由 $\frac{2 π r}{2} ＝ \sqrt{3}$ π，得r＝ $\sqrt{3}$ ，所以A选项正确；

假设该圆锥的轴截面将该圆锥分成两部分，将其中的一部分展开，则其侧面展开图是一个圆心角为 $\frac{\sqrt{3} π}{2}$ 的扇形，所以从A点经过圆锥的表面到达B点的最短距离为2×2×sin $\frac{\frac{\sqrt{3} π}{2}}{2}$ ＝4sin $\frac{\sqrt{3} π}{4}$ ≠2 $\sqrt{3}$ ，故B选项不正确；

因为r＝ $\sqrt{3}$ ，母线长为2，所以该圆锥的高为1，所以其体积为 $\frac{1}{3}$ ×π×( $\sqrt{3}$ )²×1＝π，故C选项正确；

过该圆锥的顶点作圆锥的截面，则截面为腰长为2的等腰三角形，设其顶角为θ，则该三角形的面积为S＝ $\frac{1}{2}$ ×2×2sin θ.故当θ＝ $\frac{π}{2}$ 时，

S_max＝ $\frac{1}{2}$ ×2×2×1＝2≠ $\sqrt{3}$ ，故D选项不正确.

第10题 (填空题) 难度 - 基础题：

已知球O的表面积为20π，平面α截球O所得的截面面积为3π，则以O为顶点，截面为底面的圆锥的体积为　　　　　　　.

答案:

$\sqrt{2}$ π

解析:

设球O的半径为R，截面圆O₁的半径为r，球心O到平面α的距离为d，

∵4πR²＝20π，πr²＝3π，

∴R²＝5，r²＝3，

∴d＝ $\sqrt{R^{2} - r^{2}} ＝ \sqrt{2}$ ，∴以O为顶点，截面为底面的圆锥的体积为V＝ $\frac{1}{3}$ πr²d＝ $\sqrt{2}$ π.

第11题 (填空题) 难度 - 基础题：

已知三棱锥A－BCD的三条侧棱AB，AC，AD两两互相垂直，且该三棱锥外接球的表面积为25π，且AB＝ $\sqrt{3}$ ，AD＝ $\sqrt{6}$ ，则三棱锥A－BCD的体积为　　　　　.

答案:

2 $\sqrt{2}$

解析:

因为三棱锥A－BCD的三条侧棱AB，AC，AD两两互相垂直，所以将三棱锥补成如图所示的长方体，

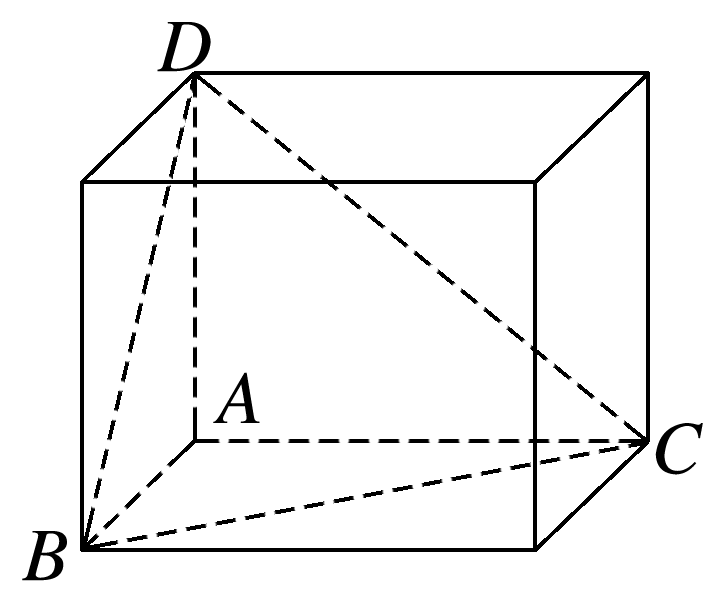
则长方体的体对角线等于三棱锥外接球的直径，因为三棱锥外接球的表面积为25π，

所以4πR²＝25π，

得R＝ $\frac{5}{2}$ ，

所以AB²＋AD²＋AC²＝(2R)²＝25，

即3＋6＋AC²＝25，得AC＝4，

所以V_三棱锥_A_－_BCD＝V_三棱锥_D_－_ABC＝ $\frac{1}{3}$ S_△_ABC·AD

＝ $\frac{1}{3}$ × $\frac{1}{2}$ × $\sqrt{3}$ ×4× $\sqrt{6}$ ＝2 $\sqrt{2}$ .

第12题 (填空题) 难度 - 基础题：

攒尖是古代中国建筑中屋顶的一种结构形式，宋代称为撮尖，清代称攒尖，依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等，也有单檐和重檐之分，多见于亭阁式建筑.如图所示，某园林建筑为六角攒尖，它的主要部分的轮廓可近似看作一个正六棱锥，若此正六棱锥的侧面等腰三角形的底角为α，则侧棱与底面外接圆的半径的比值为　　　　　.

答案:

$\frac{1}{2 c o s α}$

解析:

因为正六棱锥的底面为正六边形，

设其外接圆半径为r，则底面正六边形的边长为r，

又因为正六棱锥的侧面等腰三角形的底角为α，

所以侧棱长为 $\frac{\frac{r}{2}}{c o s α} ＝ \frac{r}{2 c o s α}$ ，所以侧棱与底面外接圆半径的比值为 $\frac{\frac{r}{2 c o s α}}{r} ＝ \frac{1}{2 c o s α}$ .

第13题 (解答题) - 简答题难度 - 基础题：

如图，一个水平放置的平面图形的直观图A'B'C'D'是边长为2的菱形，且O'D'＝2，求原平面图形的周长.

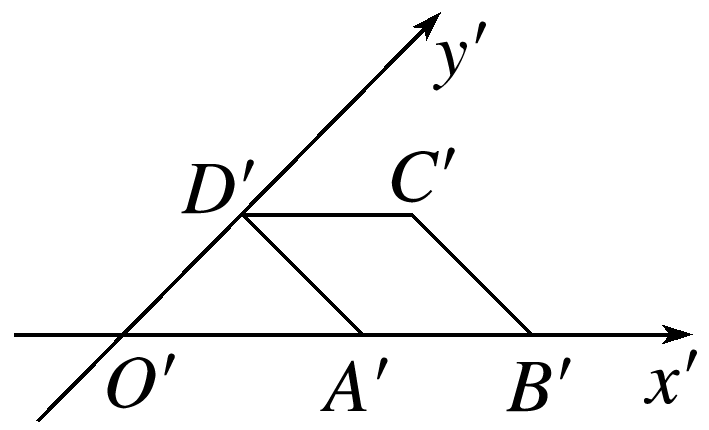
答案:

解　由题可知，O'D'＝A'D'＝2，∠A'O'D'＝45°，

∴O'A'＝2 $\sqrt{2}$ .

还原直观图可得原平面图形，如图所示，

则OD＝2O'D'＝4，OA＝O'A'＝2 $\sqrt{2}$ ，AB＝DC＝2，

∴AD＝ $\sqrt{O A^{2} ＋ O D^{2}} ＝ \sqrt{(2 \sqrt{2})^{2} ＋ 4^{2}}$ ＝2 $\sqrt{6}$ ，

∴原平面图形的周长为4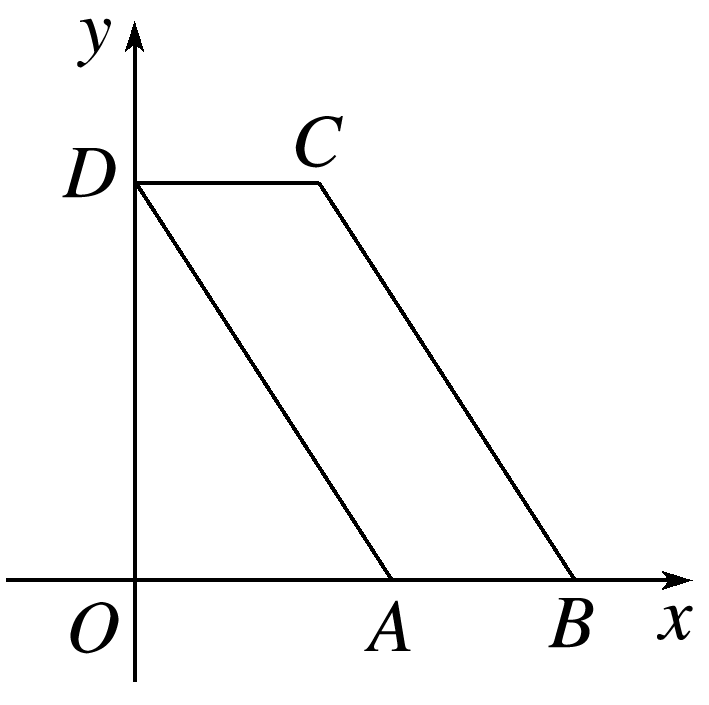 $\sqrt{6}$ ＋4.

第14题 (解答题) - 简答题难度 - 基础题：

在一个如图所示的直角梯形ABCD内挖去一个扇形，E是梯形的下底边上的一点，将所得平面图形绕直线DE旋转一圈.

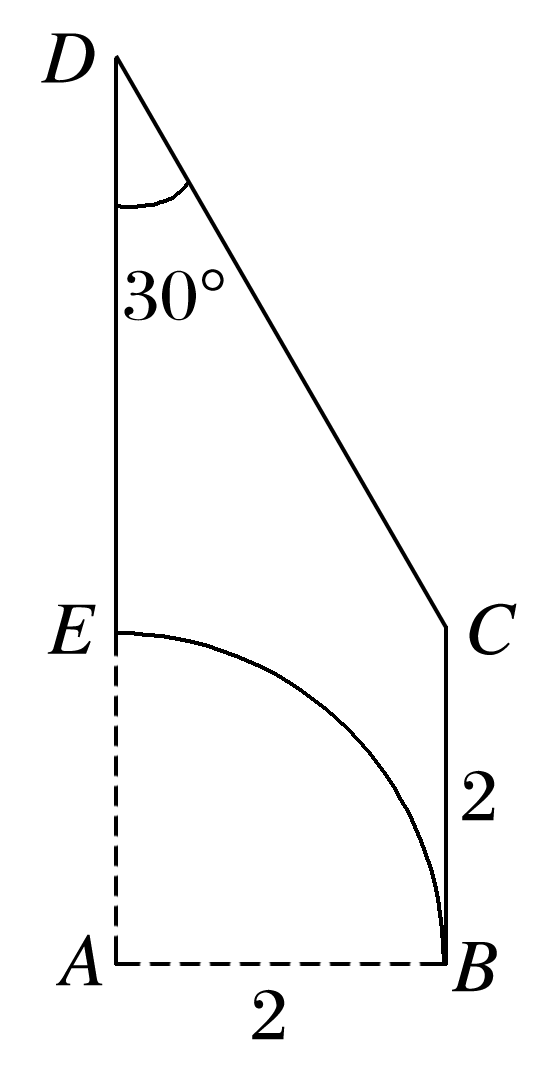
(1)说明所得几何体的结构特征；

(2)求所得几何体的表面积和体积.

答案:

解　(1)该几何体为上半部分为圆锥，下半部分为圆柱体挖去一个半球体的组合体.

(2)由图中的数据可知圆锥的底面半径为2，母线长为4，高为2 $\sqrt{3}$ ，圆柱的底面半径为2，高为2，球的半径为2，所以S_组合体＝S_圆锥侧＋S_圆柱侧＋S_半球＝π×2×4＋2π×2×2＋2π×2²＝8π＋8π＋8π＝24π，该几何体的体积为

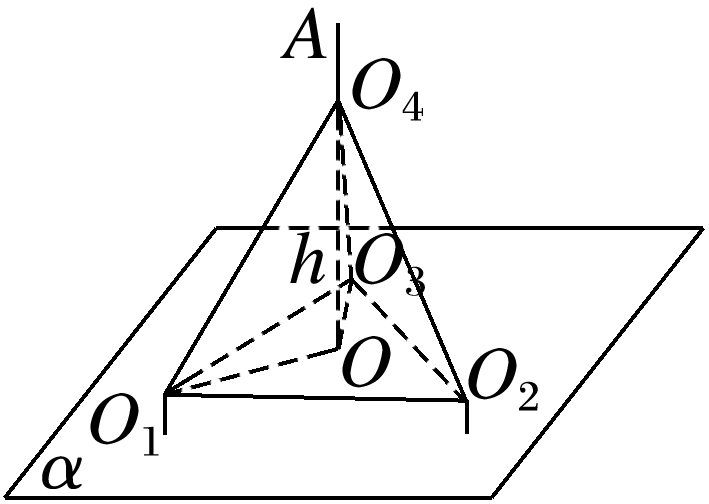
V_组合体＝V_圆锥＋V_圆柱－V_半球＝ $\frac{1}{3}$ ×π×2²×2 $\sqrt{3}$ ＋π×2²×2－ $\frac{2}{3}$ π×2³＝ $\frac{8 \sqrt{3} π ＋ 8 π}{3}$ .

第15题 (解答题) - 简答题难度 - 基础题：

将3个半径为1的球和1个半径为 $\sqrt{2}$ －1的球叠为两层放在桌面上，上层只放1个较小的球，4个球两两相切，求上层小球的最高点到桌面的距离.

答案:

解　如图，将球心O₁，O₂，O₃，O₄连接起来构成侧棱为 $\sqrt{2}$ ，底面边长为2的正三棱锥O₄－O₁O₂O₃，

设底面三角形的中心为O，

则OO₁＝ $\frac{2}{3}$ O₁O₂sin 60°＝ $\frac{2}{3}$ ×2× $\frac{\sqrt{3}}{2} ＝ \frac{2 \sqrt{3}}{3}$ ，

故正三棱锥O₄－O₁O₂O₃的高h＝ $\sqrt{O_{1} O_{4}^{2} - O O_{1}^{2}} ＝ \sqrt{{(\sqrt{2})}^{2} - {(\frac{2 \sqrt{3}}{3})}^{2}} ＝ \frac{\sqrt{6}}{3}$ ，显然平面O₁O₂O₃到桌面的距离为1，所以上层小球的最高点A到桌面的距离为1＋ $\frac{\sqrt{6}}{3} ＋ \sqrt{2}$ －1＝ $\frac{\sqrt{6}}{3} ＋ \sqrt{2}$ .

第八章 周练5(范围：§8.1~§8.3)

第八章周练5(范围：§8.1~§8.3)