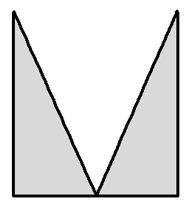
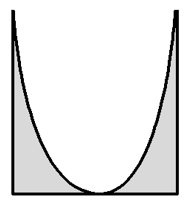
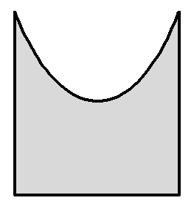
下列几何体中不是旋转体的是( )
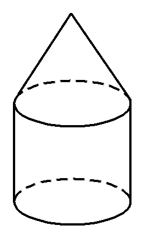
- A:
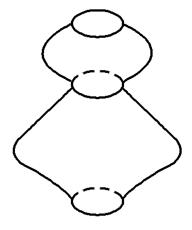
- B:
- C:
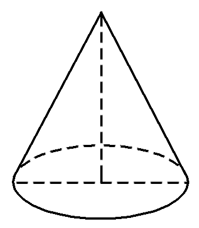
- D:
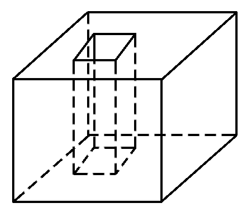
由旋转体的概念知A,B,C是旋转体,D不是旋转体.
下列几何体中不是旋转体的是( )




由旋转体的概念知A,B,C是旋转体,D不是旋转体.
一个等腰三角形绕它的底边所在直线旋转360°形成的曲面所围成的几何体是( )
过等腰三角形的顶点向底边作垂线,得到两个有一条公共边的全等直角三角形,而直角三角形以一条直角边所在直线为轴旋转一周得到的几何体是圆锥.
图①②中的图形折叠后的图形分别是( )
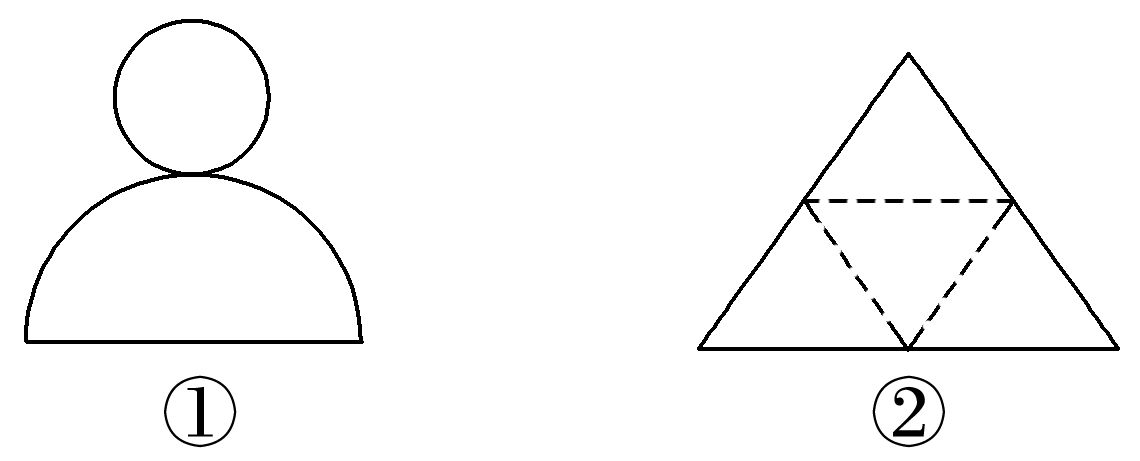
易知①为圆锥,②为三棱锥.
用长为4,宽为2的矩形作侧面围成一个圆柱,此圆柱轴截面的面积为( )
当围成的圆柱底面周长为4,高为2时,
设圆柱底面圆的半径为r,
则2πr=4,所以r=,
所以轴截面是长为2,宽为的矩形,
所以轴截面的面积为2×.
同理,当围成的圆柱底面周长为2,高为4时,轴截面的面积也为.
过球面上任意两点A,B作大圆(经过球心的截面圆),可能的个数是( )
当过A,B的直线经过球心时,经过A,B的所得的截面圆都是球的大圆,这时过A,B作球的大圆有无数个;当直线AB不经过球心O时,经过A,B,O的截面就是一个大圆,这时只能作出一个大圆.
由等腰梯形、矩形、半圆、圆、倒三角形对接形成的轴对称平面图形如图所示,若将它绕对称轴旋转180°后形成一个组合体,则下列说法不正确的是( )
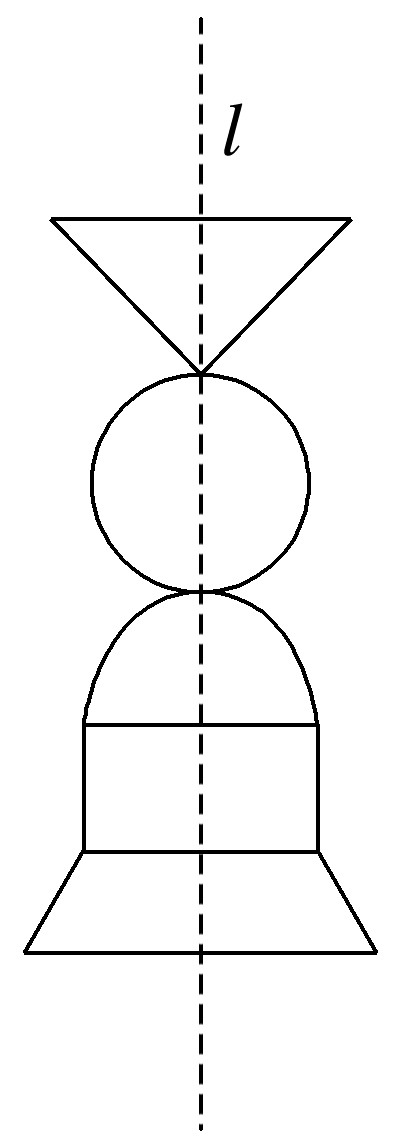
等腰梯形旋转形成的是圆台,矩形旋转形成的是圆柱,半圆旋转形成的是半球,圆旋转形成的是球,倒三角形旋转形成的是圆锥.
下列几何体中是旋转体的是( )
由旋转体的概念知A,C是旋转体.
下列说法中不正确的是( )
将正方形绕其一边所在直线旋转可以形成圆柱,所以A错误;
B中没有说明这两个平行截面的位置关系,当这两个平行截面与底面平行时正确,其他情况下结论不一定正确,所以B错误;
通过圆台侧面上一点,只有一条母线,所以D错误.
如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )
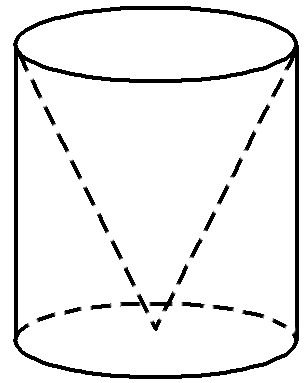

当竖直的平面经过圆锥的顶点时,截面图形如选项A中的图形,当竖直的平面不经过圆锥的顶点时,截面图形可能为选项D中的图形.
若用与球心的距离为的平面截球体所得的圆面半径为2,则球的半径为 .
答案: 3
由于球心到平面的距离为,所得圆面的半径为2,
则球的半径R==3.
轴截面是直角三角形的圆锥的底面半径为r,则其轴截面面积为 .
答案: r2
由圆锥的结构特征可知,轴截面为等腰直角三角形,其高为r,
所以S=×2r2=r2.
已知圆台的上底面半径为2 cm,下底面半径为4 cm,圆台的高为2 cm,则侧面展开图所在扇形的圆心角为 .
答案: π
把该圆台补成圆锥,所得圆锥的轴截面如图所示.过点E作EF⊥AC于点F,
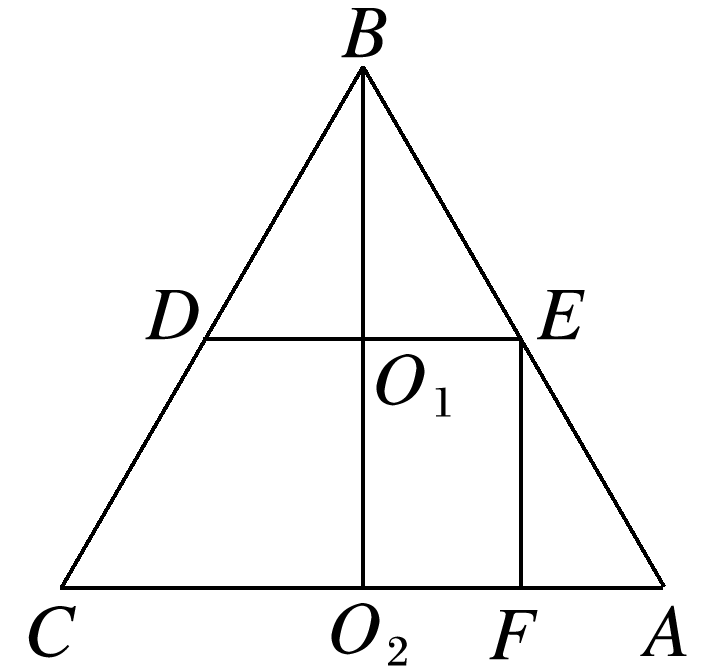
所以圆台的母线
AE=
==4(cm),
因为上底面半径长为下底面半径长的一半,
所以圆锥的母线长为8 cm,所以侧面展开图所在扇形的圆心角为=π.
有这样一个古算题:“今有木长二丈四尺,围之五尺,葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周长为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少?”这个问题中,葛藤长的最小值为 .(注:1丈等于10尺)
答案: 2丈6尺
如图,
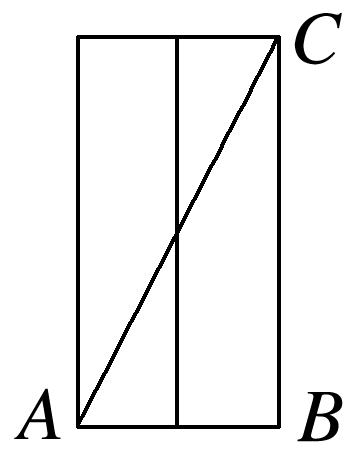
在Rt△ABC中,BC(即圆木的高)长24尺,AB=5×2=10(尺),因此葛藤长的最小值为=26(尺),即2丈6尺.
(课本P104练习T3)如图,以△ABC的一边AB所在直线为轴,其余两边旋转一周形成的面围成一个几何体,说出这个几何体的结构特征.
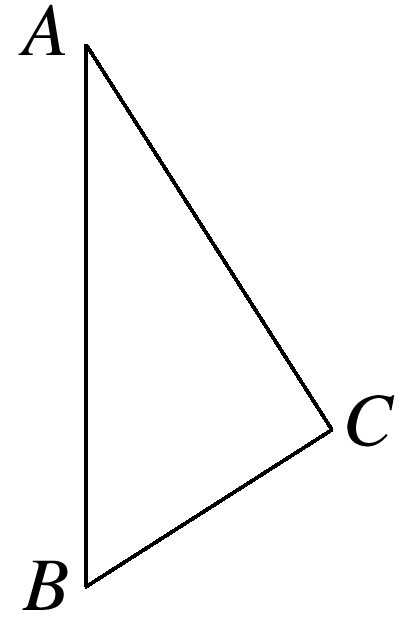
答案: 解 可以把三角形看作由两个直角三角形拼接而成, 作CD⊥AB于D(图略),则以△ABC的一边AB所在直线为轴,其余两边旋转一周形成的面围成一个几何体可以看作由两个直角三角形绕各自的直角边旋转而成,直角三角形绕直角边旋转可得圆锥,所以形成的几何体是两个同底的圆锥.
已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面得到圆M.
(1)若OA=1,求圆M的面积;
(2)若圆M的面积为3π,求OA.
答案: 解 (1)若OA=1,则OM=, 故圆M的半径r=,所以圆M的面积S=πr2=. (2)因为圆M的面积为3π,所以圆M的半径R=,则OA2=+3,所以OA2=3, 解得OA=2.
国庆节期间,要在一圆锥形建筑物上挂一宣传标语,经测量得圆锥的母线长为3米,高为2 米,如图所示.为了美观,需要在底面圆周上找一点M拴系彩绸的一端,沿圆锥的侧面绕一周挂彩绸,彩绸的另一端仍回到原处M,则彩绸最短要多少米?
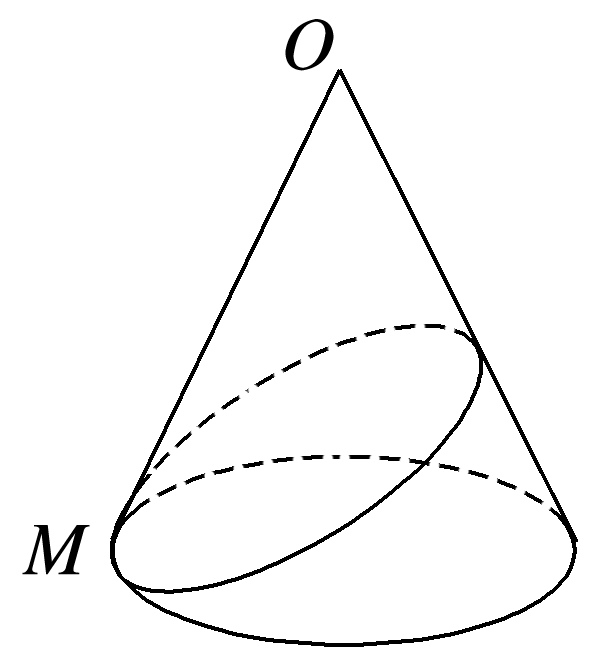
答案: 解 把圆锥的侧面沿过点M的母线剪开,并铺平得扇形MOM1,如图所示. 这样把空间问题转化为平面问题,易知彩绸的最短长度即为线段MM1的长度,由母线长为3米,高为2 米,得底面半径为1米,所以底面周长为2π×1=2π(米),扇形圆心角为180°×=120°,所以MM1=3 米,即彩绸最短要3米.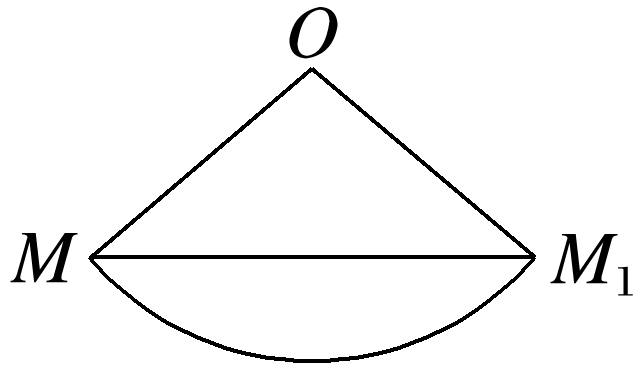
一个正方体内接于一个球,过球心作一截面,则截面的图形可能是( )
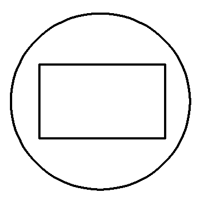
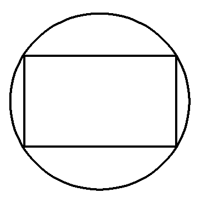
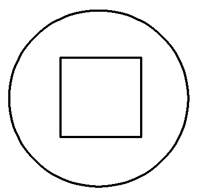
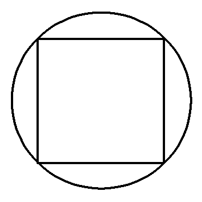
当截面平行于正方体的一个侧面时得C,当截面过正方体的对角线时得B,当截面不平行于任何侧面也不过对角线时得A,但无论如何都不能截出D.
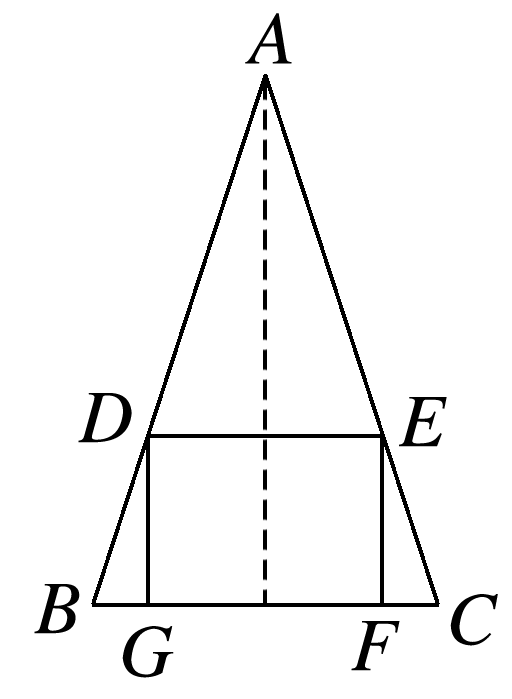
已知一个圆锥的底面半径为r,高为h,在此圆锥内有一个内接正方体,这个内接正方体的顶点在圆锥的底面和侧面上,求此正方体的棱长.
答案: 解 作出圆锥的一个轴截面如图所示, 其中AB,AC为母线,BC为底面直径,DG,EF是正方体的棱,DE,GF是正方体的上、下底面的对角线. 设正方体的棱长为x, 则DG=EF=x,DE=GF=x. 依题意,得△ABC∽△ADE, ∴, 解得x=, 即此正方体的棱长为.