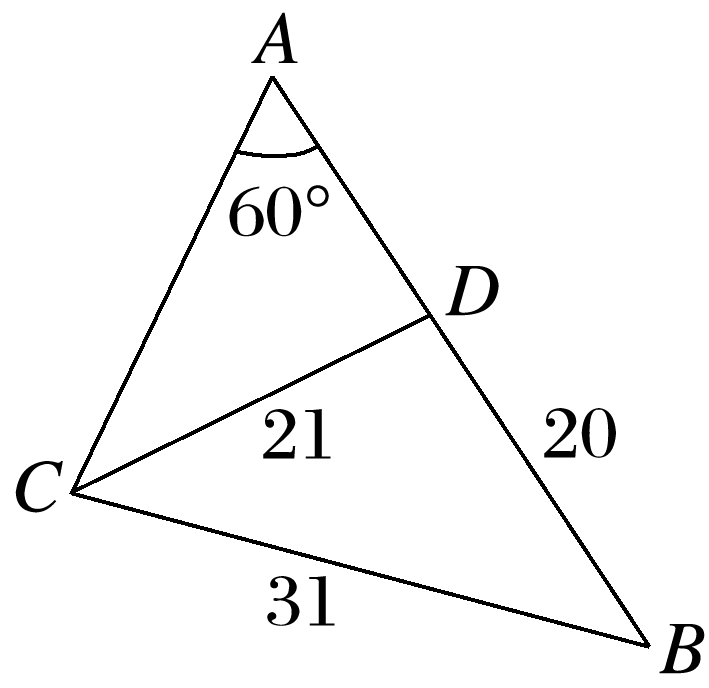
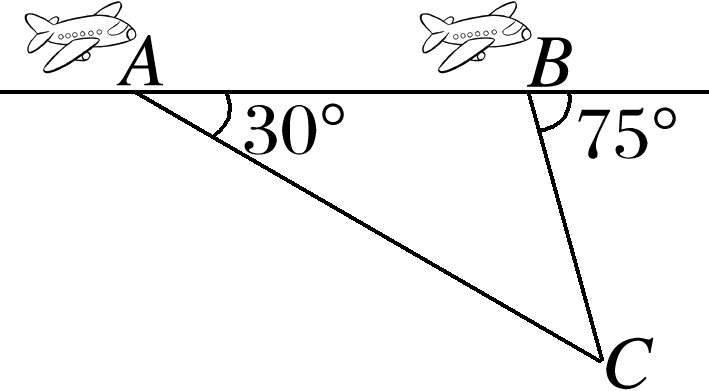
已知飞机的飞行航线AB和地面目标C在同一铅直平面内,如图所示,在A处测得目标C的俯角为30°,飞行26 km到达B处,测得目标C的俯角为75°,此时B处与地面目标C的距离为( )
- A: 13 km
- B: 5 km
- C: 5 km
- D: 13 km
在△ABC中,∠BAC=30°,∠ABC=180°-75°=105°,所以C=180°-30°-105°=45°,由正弦定理得=,
则BC=·sin 30°=×=13(km).
在△ABC中,若A=60°,a=2,则等于( )
由正弦定理得===4.
在△ABC中,a,b,c分别为角A,B,C的对边,A=60°,b=1,这个三角形的面积为,则a等于( )
依题意,得S=bcsin A=×1×csin 60°=,解得c=4,由余弦定理,
得a==.
在△ABC中,内角A,B,C所对的边分别为a,b,c.若a=4,b=5,c=6,则的值为( )
由余弦定理的推论,
得cos A===,
所以====1.
已知飞机的飞行航线AB和地面目标C在同一铅直平面内,如图所示,在A处测得目标C的俯角为30°,飞行26 km到达B处,测得目标C的俯角为75°,此时B处与地面目标C的距离为( )

在△ABC中,∠BAC=30°,∠ABC=180°-75°=105°,所以C=180°-30°-105°=45°,由正弦定理得=,
则BC=·sin 30°=×=13(km).
记△ABC的内角A,B,C的对边分别为a,b,c,若cos C=,a=3b,则cos A等于( )
因为cos C=,a=3b,
由余弦定理c2=a2+b2-2abcos C,
得c2=9b2+b2-2×3b×b×=6b2,
所以cos A===-.
在△ABC中,内角A,B,C所对的边分别为a,b,c,若S△ABC=2,a+b=6,=2cos C,则c等于( )
由正弦定理,得===1,
即2cos C=1,可得C=60°,又S△ABC=2,
所以absin C=2,
即ab=8,又a+b=6,
由余弦定理,得c2=a2+b2-2abcos C=(a+b)2-2ab-ab=(a+b)2-3ab=62-3×8=12,
解得c=2.
(多选)在△ABC中,内角A,B,C所对的边分别为a,b,c.下列各组条件中使得△ABC恰有一个解的是( )
对于A,b>a,所以B>A,又A=,所以B>,这与A+B+C=π矛盾,所以△ABC无解;
对于B,由正弦定理=,可得sin B=1,即B=,所以△ABC只有一解;
对于C,由正弦定理=,可得sin B=>sin ,又a<b,所以B有两解,
即△ABC有两解;
对于D,由正弦定理=,可得sin B=<sin ,又a>b,所以B只有一解,即△ABC只有一解.
(多选)已知△ABC的内角A,B,C所对的边分别为a,b,c,下列说法正确的是( )
对于A,因为·>0,即||||cos A>0,cos A>0,所以A是锐角,但B,C是否都为锐角,不确定,A错误;
对于B,由正弦定理得=,因此sin A>sin B⇔a>b,B正确;
对于C,因为acos C=b+,
由余弦定理得a·=b+,
化简得a2-b2-c2=bc,
所以cos A==-,
又A∈(0,π),所以A=,C正确;
对于D,由正弦定理得=,即sin B===,而0°<B<180°,又由b>a得B>A,因此B=45°或135°,所以△ABC有两解,D错误.
(多选)在锐角△ABC中,角A,B,C的对边分别是a,b,c,若a-2ccos B=c,则下列结论正确的是( )
因为a-2ccos B=c,所以由余弦定理的推论得a-2c·=c,整理得b2=c(a+c),故A正确;
因为a-2ccos B=c,所以由正弦定理得sin A-2sin Ccos B=sin C,即sin(B+C)-2sin Ccos B=sin C,所以sin(B-C)=sin C,因为C∈,
B-C∈,所以B-C=C,即B=2C,故B正确;
由△ABC为锐角三角形,
得C∈,B=2C∈,
A=π-B-C=π-3C∈,
所以C∈,所以<sin C<,故C错误;
因为a-2ccos B=c,所以=2cos B+1=3-4sin2C,因为C∈,所以∈(1,2),故D正确.
在△ABC中,内角A,B,C所对的边分别为a,b,c,若a(sin A-sin B)=(c-b)(sin B+sin C),c=2,则△ABC的外接圆的面积等于 .
答案:
由题可知,a(a-b)=(c-b)(b+c),
整理得a2+b2-c2=ab,
所以cos C==,
又0<C<π,所以C=.
所以外接圆的直径2R==,
即R=,故外接圆的面积等于.
在△ABC中,内角A,B,C所对的边分别为a,b,c,向量m=(bsin C,a),n=.已知a=4,且m∥n,则b2+c2= .
答案: 24
因为向量m=(bsin C,a),
n=,m∥n,
所以2bsin Ccos A=asin A,由正弦定理及a=4可知,2bccos A=a2=8,由余弦定理可得b2+c2-a2=2bccos A=8,则b2+c2=a2+8=24.
江岸边有一炮台高30 m,江中有两条船,由炮台顶部测得两条船的俯角分别为45°与60°,且两条船与炮台底部的连线成30°角,则两条船之间的距离为 m.
答案: 10
设炮台顶部为A,两条船分别为B,C,炮台底部为D(如图),则∠BAD=45°,∠CAD=30°,∠BDC=30°,AD=30 m.
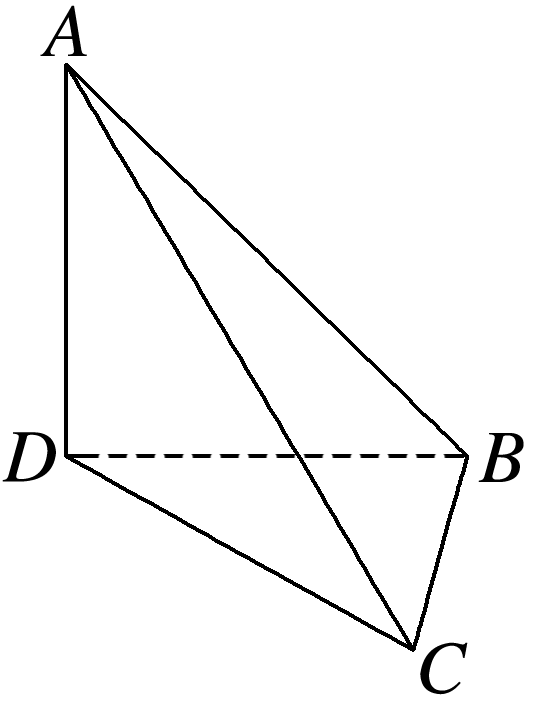
在Rt△ABD与Rt△ACD中,tan 45°=,tan 30°=,
则DB=30 m,DC=10 m.
在△DBC中,由余弦定理BC2=DB2+DC2-2DB·DCcos 30°,得BC2=302+(10)2-2×30×10×=300,解得BC=10 m.
在△ABC中,BC=,AC=3,sin C=2sin A.
(1)求AB的值;
(2)求sin的值.
答案: 解 (1)在△ABC中,由正弦定理,得 AB=·BC=2BC=2. (2)在△ABC中,根据余弦定理的推论, 得cos A==, ∴sin A==, ∴sin 2A=2sin Acos A=, cos 2A=cos2A-sin2A=, ∴sin=sin 2Acos -cos 2Asin =.
(2024·新课标全国Ⅱ)记△ABC的内角A,B,C的对边分别为a,b,c,已知sin A+cos A=2.
(1)求A;
(2)若a=2,bsin C=csin 2B,求△ABC的周长.
答案: 解 (1)方法一 常规方法(辅助角公式) 由sin A+cos A=2, 可得sin A+cos A=1, 即sin=1, 由于A∈(0,π)⇒A+∈, 故A+=, 解得A=. 方法二 常规方法(同角三角函数的基本关系) 由sin A+cos A=2, 又sin 2A+cos 2A=1, 消去sin A得到 4cos2A-4cos A+3=0⇔(2cos A-)2=0, 解得cos A=, 又A∈(0,π),故A=. (2)由题设条件和正弦定理得, bsin C=csin 2B⇔sin Bsin C =2sin Csin Bcos B, 又B,C∈(0,π),则sin Bsin C≠0, 进而cos B=,得到B=, 于是C=π-A-B=, sin C=sin(π-A-B)=sin(A+B) =sin Acos B+cos Asin B =, 由正弦定理可得, ==, 即==, 解得b=2,c=+, 故△ABC的周长为2++3.
如图,目标A在某观测站C的北偏东25°方向,从A出发有一条南偏东35°走向的公路.在C处测得与C相距31千米的公路上的B处有一人正沿此公路向A走去,走20千米到达D处,此时测得CD为21千米.
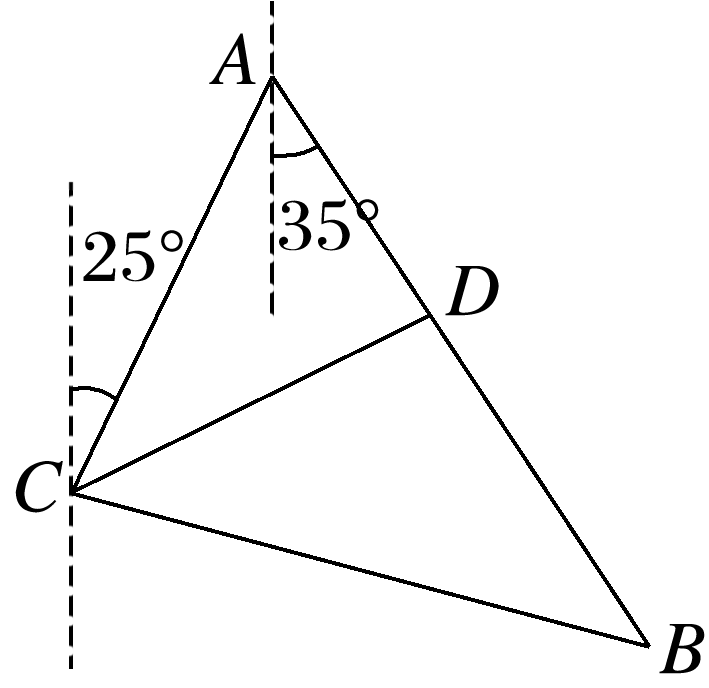
(1)求sin B的值;
(2)求A,C两处的距离.
答案: 解 (1)根据题意,如图,在△BCD中,BC=31, BD=20,CD=21, 所以cos B====, 所以sin B==. (2)在△ABC中,由正弦定理=, 得AC===24. 即A,C两处的距离为24千米.