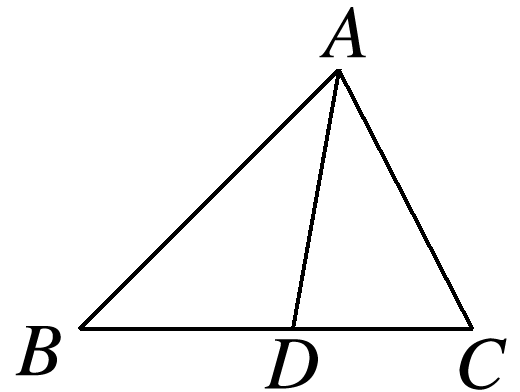
如图,在△ABC中,B=45°,AC=8,D是BC边上一点,DC=5,DA=7,则AB的长为( )
- A: 4
- B: 4
- C: 8
- D: 4
在△ADC中,因为DC=5,DA=7,AC=8,
所以cos∠ADC==,
因此cos∠ADB=-,所以sin∠ADB=,
在△ABD中,又B=45°,
由正弦定理=,
得AB===4.
已知△ABC中,内角A,B,C对应的边分别为a,b,c,若a+b=4,c=,C=,则△ABC的面积为( )
由余弦定理可得7=a2+b2-2abcos C=(a+b)2-3ab=16-3ab,所以ab=3.
所以S=absin C=×3×=.
在△ABC中,角A,B,C所对的边分别为a,b,c,若c=2acos B,则△ABC的形状一定是( )
∵c=2acos B,∴由正弦定理得2cos Bsin A=sin C,即2cos Bsin A=sin(A+B)
=cos Bsin A+cos Asin B,
∴sin Acos B-cos Asin B=0,即sin(A-B)=0,
又∵-π<A-B<π,∴A-B=0,∴A=B.
∴△ABC是等腰三角形.
在△ABC中,a,b,c分别是角A,B,C的对边,B=,且sin A=2sin C,则的值为( )
因为sin A=2sin C,
所以由正弦定理可得a=2c,
又由余弦定理得b2=a2+c2-2accos =3c2,
所以b=c,即=.
在△ABC中,角A,B,C所对的边分别为a,b,c,若b=5,C=60°,且△ABC的面积为5,则△ABC的周长为( )
由题意及三角形的面积公式,得absin C=5,即a×5×=5,解得a=4,根据余弦定理得c2=a2+b2-2abcos C=16+25-2×4×5×=21,即c=,
所以△ABC的周长为9+.
如图,在△ABC中,B=45°,AC=8,D是BC边上一点,DC=5,DA=7,则AB的长为( )

在△ADC中,因为DC=5,DA=7,AC=8,
所以cos∠ADC==,
因此cos∠ADB=-,所以sin∠ADB=,
在△ABD中,又B=45°,
由正弦定理=,
得AB===4.
已知△ABC中,角A,B,C所对的边分别为a,b,c,若△ABC的面积为,cos C=1-,则C的值为( )
由题意得,在△ABC中,ab=,
则S△ABC=absin C==,
因为0<C<π,
则0<<,则tan >0,
所以==,
可得tan =,所以=,
故C=.
(多选)在△ABC中,内角A,B,C的对边分别为a,b,c,已知a=3,b=4,锐角C满足sin C=,则下列结论正确的是( )
在△ABC中,因为a=3,b=4,
且sin C=,
则S△ABC=absin C=×3×4×=,所以A错误;
由C为锐角,且sin C=,
可得cos C==,所以B正确;
由余弦定理得c2=a2+b2-2abcos C
=9+16-2×3×4×=19,
可得c=,所以C正确;
由余弦定理的推论得
cos B===,所以D错误.
(多选)在△ABC,下列说法正确的是( )
选项A,当a=6,b=4,c=9时,
a2=bc,此时cos C==-<0,
则<C<π,△ABC为钝角三角形,故A错误;
对于B,a2tan B=b2tan A⇒sin2A·=sin2B·,
即sin Acos A=sin Bcos B,
即sin 2A=sin 2B,
所以sin 2A=sin 2B,而A,B为三角形内角,
所以2A=2B⇒A=B或者
2A+2B=π⇒A+B=,
所以△ABC是等腰三角形或者直角三角形,故B错误;
对于C,因为△ABC是锐角三角形,
所以A+B>,即>A>-B>0,
由正弦函数性质结合诱导公式得
sin A>sin=cos B,故C正确;
对于D,由<cos A可得
c<bcos A⇒sin C<sin Bcos A⇒sin(B+A)
=sin Bcos A+cos Bsin A<sin Bcos A,
所以cos Bsin A<0,
由于A,B∈(0,π),所以sin A>0,
进而cos B<0,故B∈,
因此三角形为钝角三角形,故D正确.
(多选)在△ABC中,内角A,B,C所对的边分别为a,b,c,B=,BC边上的高等于,则以下四个结论正确的是( )
如图,过点A作AD⊥BC于点D,所以AD=,
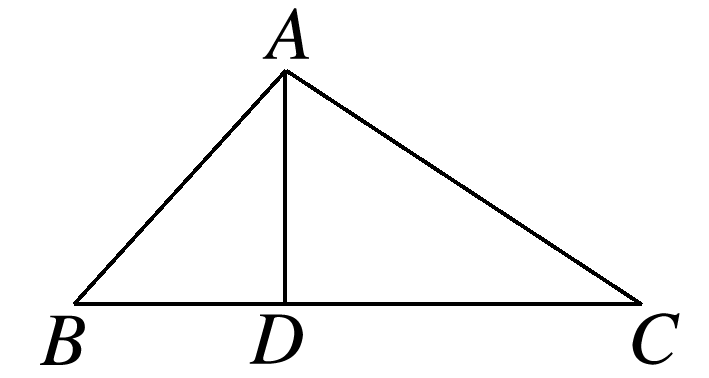
由B=,可得BD=,CD=,c=AB=a,
b=AC=a,
所以cos C===,故A正确;
由cos C=,可得sin C=,
由=,
可得sin∠BAC=,故B正确;
由tan∠DAC==2,所以∠DAC>,
而∠BAD=,所以∠BAC>,
所以cos∠BAC=-,tan∠BAC=-3,故C错误;
又b2-c2=-=,故D正确.
若在△ABC中,C=30°,a+b=1,则△ABC面积S的最大值是 .
答案:
由题意,得ab≤(a+b)2=,
当且仅当a=b=时等号成立,
故S=absin C≤××=.
已知在△ABC中,AC=2,AB=3,∠BAC=60°,AD是∠BAC的平分线,则AD= .
答案:
如图,∵S△ABC=S△ABD+S△ACD,
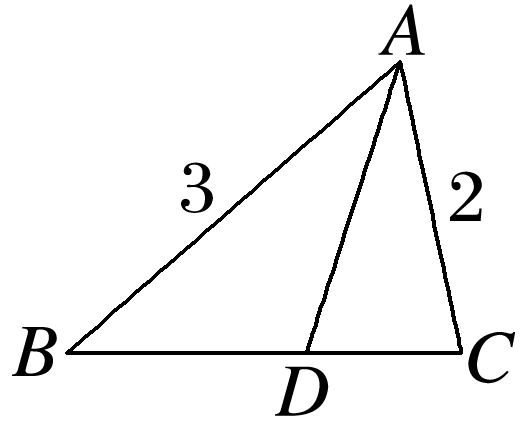
∴×3×2×sin 60°=×3AD×sin 30°+×2AD×sin 30°,∴AD=.
在△ABC中,角A,B,C的对边分别为a,b,c,若A=,a2+b2-c2=ab,c=3,则C= ,a= .
答案:
由a2+b2-c2=ab,
得cos C==,
∵C∈(0,π),∴C=,
由正弦定理=,
得a===.
在△ABC中,a,b,c分别为角A,B,C的对边,若B=,a2+c2=4ac,则= .
答案:
由已知及余弦定理,
得b2=a2+c2-2accos B=5ac,
则由正弦定理,得sin2B=5sin Asin C=,
所以sin Asin C=,
所以==.
在△ABC中,内角A,B,C的对边分别为a,b,c,且sin 2B=sin B.
(1)求B的大小;
(2)若△ABC的面积为6,a=4,求b的长.
答案: 解 (1)因为sin 2B=sin B,所以2sin Bcos B=sin B. 因为sin B≠0,所以cos B=,又0<B<π,所以B=. (2)因为S△ABC=acsin B=×4×c×=6,所以c=3. 由余弦定理得b2=a2+c2-2accos B=16+18-2×4×3×=10, 所以b=.
已知在△ABC中,角A,B,C所对的边分别为a,b,c,且acos C+c=b.
(1)求A的大小;
(2)若a=1,b=,求c的值.
答案: 解 (1)由acos C+c=b, 得sin Acos C+sin C=sin B. 因为sin B=sin(A+C)=sin Acos C+cos Asin C, 所以sin C=cos Asin C. 因为sin C≠0,所以cos A=. 因为0<A<π,所以A=. (2)由正弦定理,得sin B==. 所以B=或. ①当B=时,由A=,得C=, 所以c=2; ②当B=时, 由A=,得C=, 所以c=a=1.综上可得,c=1或2.
已知锐角△ABC的内角A,B,C的对边分别为a,b,c,且bcos C+ccos B=2acos A.
(1)求角A的大小;
(2)若b=2,求△ABC面积的取值范围.
答案: 解 (1)因为bcos C+ccos B=2acos A, 由正弦定理,可得sin Bcos C+sin Ccos B=2sin Acos A, 即sin(B+C)=2sin Acos A, 即sin A=2sin Acos A, 因为在锐角△ABC中,0<A<, 所以sin A≠0,所以cos A=, 所以A=. (2)由正弦定理=,得c=, S△ABC=bcsin A=c=, 因为A=,所以C=-B, 所以S△ABC== =·+,因为△ABC为锐角三角形, 所以解得<B<, 则tan B∈,所以S△ABC∈, 故△ABC面积的取值范围是.
(多选)如图,△ABC的内角∠CAB,B,∠ACB所对的边分别为a,b,c,(acos∠ACB+ccos∠CAB)=2bsin B,且∠CAB=.若D是△ABC外一点,DC=1,AD=3,则下列说法中正确的是( )
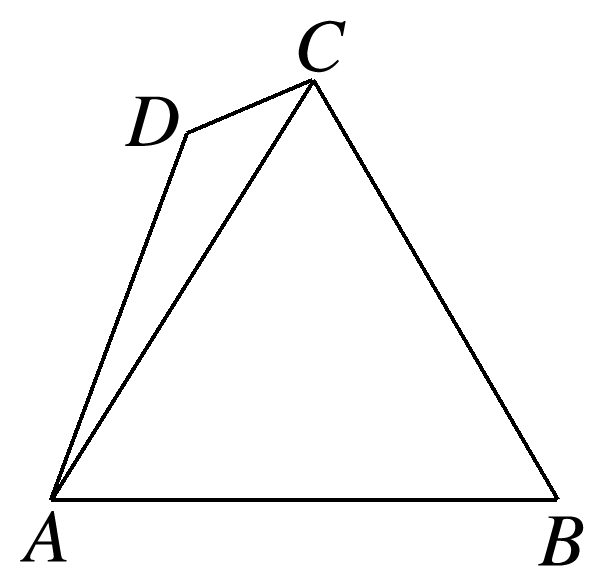
∵(acos∠ACB+ccos∠CAB)=2bsin B,
∴(sin∠CABcos∠ACB+sin∠ACBcos∠CAB)=2sin2B,
∴sin(∠CAB+∠ACB)=2sin2B,
∴sin B=2sin2B.
又sin B≠0,∴sin B=.
∵∠CAB=,∴B∈,
∴B=,∴∠ACB=π-∠CAB-B=,因此A,B正确;
四边形ABCD的面积等于S△ABC+S△ACD=AC2+AD·DCsin∠ADC=(AD2+DC2-2AD·DCcos∠ADC)+AD·DCsin∠ADC=(9+1-6cos∠ADC)+×3×1×sin∠ADC=+3sin≤+3,当且仅当∠ADC-=,即∠ADC=时,等号成立,因此C正确,D错误.
如图在五边形ABCDE中,CD=3AB=3BC=,∠ABC=∠BCD=,∠AED=.
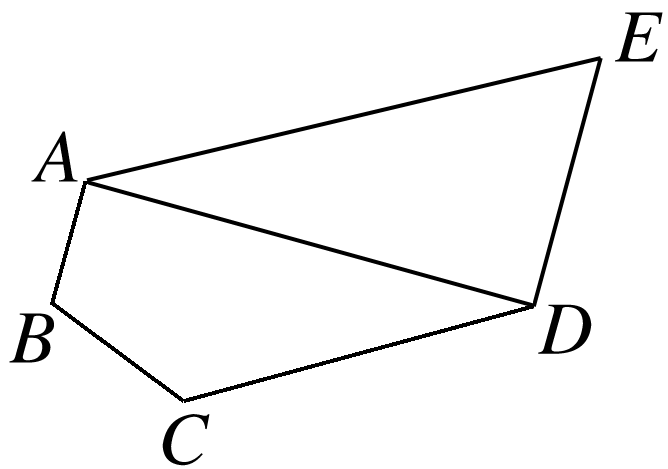
(1)求线段AD的长;
(2)设∠DAE=α, △ADE的面积为S,则S=f(α),求f(α)的表达式.
答案: 解 (1)方法一 由题意可得与的夹角是,与的夹角是,与的夹角是,又知AB=BC=,CD=, 可求得·=,·=, ·=-. 因为=++,所以有 ==+++2·+2·+2· =+++2=, 所以AD=. 方法二 连接AC(图略),在△ABC中,AC2=AB2+BC2-2AB·BCcos∠ABC=, 所以AC=. 因为AB=BC,所以∠BAC=∠ACB=, 因为∠BCD=,所以∠ACD=,即AC⊥CD. 在Rt△ACD中,AD===. (2)在△ADE中,因为∠DAE=α,∠AED=, 所以∠ADE=-α. 由正弦定理得===,所以AE=sin,DE=sin α, 所以S=f(α)=AE·DEsin =sinsin α=.