设非零向量=a,=b,=a+b,满足|a|=|b|,|a+b|=|a-b|,则四边形ABCD的形状为( )
- A: 平行四边形
- B: 矩形
- C: 正方形
- D: 菱形
如图,
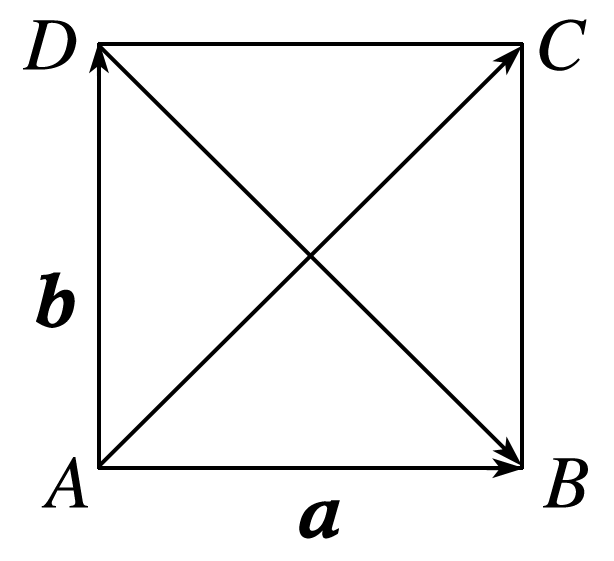
因为=a,=b,
所以-==a-b,
由=a+b,得四边形ABCD为平行四边形,
又因为|a+b|=|a-b|,
所以||=||,又因为|a|=|b|,所以四边形ABCD是正方形.
化简2(b+a)+b-3(a-b)的结果是( )
原式=2b+2a+b-3a+3b=-a+6b.
已知单位向量a,b,则(2a+b)·(2a-b)的值为( )
由题意得(2a+b)·(2a-b)=4a2-b2=4-1=3.
(2024·新课标全国Ⅱ)已知向量a,b满足|a|=1,|a+2b|=2,且(b-2a)⊥b,则|b|等于( )
因为(b-2a)⊥b,
所以(b-2a)·b=0,
即b2=2a·b,
又因为|a|=1,|a+2b|=2,
所以1+4a·b+4b2=1+6b2=4,
从而|b|=.
设非零向量=a,=b,=a+b,满足|a|=|b|,|a+b|=|a-b|,则四边形ABCD的形状为( )
如图,

因为=a,=b,
所以-==a-b,
由=a+b,得四边形ABCD为平行四边形,
又因为|a+b|=|a-b|,
所以||=||,又因为|a|=|b|,所以四边形ABCD是正方形.
已知向量a,b满足|a|=5,|b|=6,a·b=-6,则cos〈b,a+b〉等于( )
因为|a|=5,|b|=6,a·b=-6,
所以b·(a+b)=a·b+b2=a·b+|b|2=-6+36=30,
|a+b|==
===7,
所以cos〈b,a+b〉===.
已知△ABC和点M满足++=0,若存在实数λ使得+=λ成立,则λ等于( )
由++=0,
可知M为△ABC的重心,取BC的中点N(图略),则有=,
所以+=λ=2=2×=3,则λ=3.
(多选)已知非零向量e1,e2,a,b满足a=2e1-e2,b=ke1+e2(k∈R),则以下结论正确的是( )
非零向量e1,e2,a,b满足a=2e1-e2,
b=ke1+e2(k∈R),若e1与e2不共线,
a与b共线,可得λa=b(λ∈R),
即2λ=k,-λ=1,解得k=-2.
所以A正确,B错误;
若e1与e2共线,可得e1=me2(m∈R),a=2e1-e2=(2m-1)e2,b=ke1+e2=(km+1)e2,可得a与b共线,所以C错误,D正确.
(多选)在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E是CD的中点,则( )
对于A,=+=+,所以A正确;
对于B,由AB=4,AD=2,∠BAD=60°,
可得||=4,||=2,·=4,
则||2==+·+=×42+4+4=12,
所以||=2,所以B正确;
对于C,由=+,
=-,
可得·=·(-)
=--·+=-6,
所以C正确;
对于D,由在上的投影向量为·=·=,
所以D不正确.
(多选)已知向量a,b满足|a|=1,|b|=2,|a+b|=2,则下列结论中正确的是( )
∵|a+b|2=a2+2a·b+b2=1+2a·b+4=4,∴a·b=-,A错误;
∵a·(a+2b)=a2+2a·b=1+2×=0,
∴a⊥,B正确;
又|a-b|==,C正确;
∵cos〈a,b〉==-,∴a与b的夹角不是, D错误.
已知非零向量a,b,c,若向量p=++,则|p|的取值范围是 .
答案: [0,3]
由,,分别表示a,b,c方向上的单位向量,
当,,对应起止点依次首尾相连构成封闭三角形时,
p=++=0,
此时|p|最小,|p|min=0;
当,,同向共线时,
p=++=,
此时|p|最大,|p|max=3;
所以|p|的取值范围是[0,3].
已知非零向量a,b,c满足a·b=a·c,a与c的夹角为,|c|=2,则向量b在向量a上的投影向量的模为 .
答案: 1
由题设,|a||b|cos〈a,b〉=|a||c|cos〈a,c〉,
则|b|cos〈a,b〉=|c|cos〈a,c〉=-1,
而向量b在向量a上的投影向量为·a=-,
∴向量b在向量a上的投影向量的模为1.
如图,在△ABC中,若AB=AC=3,cos∠BAC=,=2,则·= .
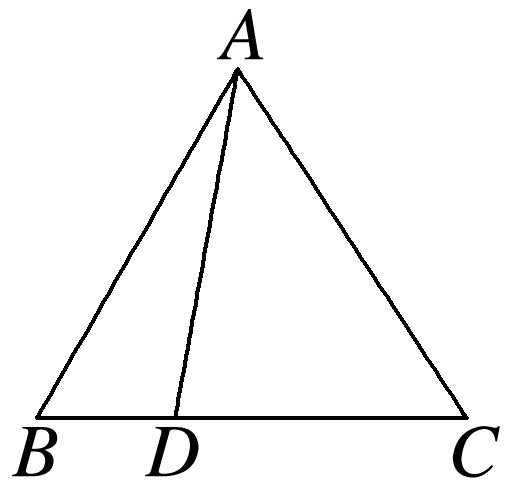
答案: -
根据条件,得
=+=+
=+-)=+,
所以·=·(-)
=·-+
=×3×3×-×9+×9=-.
已知向量e1,e2,且|e1|=|e2|=1,e1与e2的夹角为,m=λe1+e2,n=3e1-2e2.
(1)求证:(2e1-e2)⊥e2;
(2)若|m|=|n|,求λ的值.
答案: (1)证明 因为|e1|=|e2|=1, e1与e2的夹角为, 所以e1·e2=|e1||e2|cos〈e1,e2〉 =1×1×cos=, 所以(2e1-e2)·e2=2e1·e2-=2×-12=0,所以(2e1-e2)⊥e2. (2)解 由(1)知,e1·e2=, 因为|e1|=|e2|=1,|m|=|n|, 所以(λe1+e2)2=(3e1-2e2)2, 即λ2+2λe1·e2+=9-12e1·e2+4, 于是有λ2×12+2λ×+12=9×12-12×+4×12=7, 即λ2+λ-6=(λ+3)(λ-2)=0, 解得λ=-3或λ=2.
已知|a|=4,|b|=2,且a与b的夹角为120°,求:
(1)(a-2b)·(a+b);
(2)|2a-b|;
(3)a与a+b的夹角.
答案: 解 (1)a·b=4×2×cos 120°=-4, 所以(a-2b)·(a+b)=a2-a·b-2b2=16+4-8=12. (2)因为(2a-b)2=4a2-4a·b+b2=64+16+4=84,所以|2a-b|=2. (3)因为(a+b)2=a2+2a·b+b2=16-8+4=12,所以|a+b|=2, 又a·(a+b)=a2+a·b=16-4=12, 所以cos〈a,a+b〉===, 因为a与a+b的夹角范围为[0,π],所以a与a+b的夹角为.
如图所示,在△ABC中,D,F分别是BC,AC的中点,=,=a,=b.
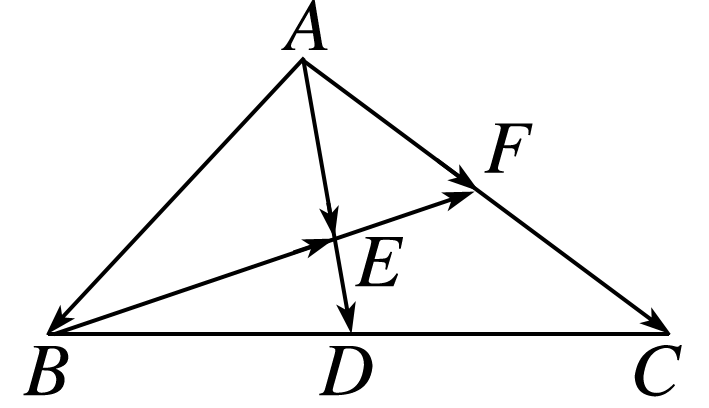
(1)用a,b表示向量,,,,;
(2)求证:B,E,F三点共线.
答案: (1)解 ∵=+)=(a+b), ∴==(a+b), ∵==b, ∴=-=(a+b)-a=(b-2a), =-=b-a=(b-2a). (2)证明 由(1)知=(b-2a), =(b-2a), ∴=,∴与共线. 又BE,BF有公共点B,∴B,E,F三点共线.