第六章作业6 向量的数量积(二)

第1题 (单选题) 难度 - 基础题：

已知单位向量a，b满足a⊥(a-b)，则向量a与b的夹角是(　　)

A: 0
B: $\frac{π}{3}$
C: $\frac{2 π}{3}$
D: $\frac{5 π}{6}$

解析:

由题设知a·(a-b)=a²-a·b=0，

又a，b为单位向量，

∴1-cos〈a，b〉=0，

即cos〈a，b〉=1，而〈a，b〉∈[0，π]，

∴〈a，b〉=0，

即向量a与b的夹角是0.

第2题 (单选题) 难度 - 基础题：

已知a，b方向相同，且|a|=2，|b|=4，则|2a+3b|等于(　　)

A: 16
B: 256
C: 8
D: 64

解析:

方法一　∵|2a+3b|²=4a²+9b²+12a·b=16+144+96=256，∴|2a+3b|=16.

方法二　由题意知2a=b，

∴|2a+3b|=|4b|=4|b|=16.

第3题 (单选题) 难度 - 基础题：

已知向量a，b的夹角为45°，且|a|=4， $(\frac{1}{2} a + b)$ · $(2 a - 3 b)$ =12，则b在a上的投影向量为(　　)

A: $\frac{1}{4}$ a
B: 2b
C: $\sqrt{2}$ a
D: 2 $\sqrt{2}$ b

解析:

$(\frac{1}{2} a + b)$ ·(2a-3b)=a²+ $\frac{1}{2}$ a·b-3b²=|a|²+ $\frac{1}{2}$ |a||b|cos 45°-3|b|²=16+ $\sqrt{2}$ |b|-3|b|²=12，

解得|b|= $\sqrt{2}$ 或|b|=- $\frac{2 \sqrt{2}}{3}$ (舍去).故b在a上的投影向量为|b|cos 45° $\frac{a}{| a |}$ = $\sqrt{2}$ × $\frac{\sqrt{2}}{2}$ × $\frac{a}{4}$ = $\frac{1}{4}$ a.

第4题 (单选题) 难度 - 基础题：

已知向量a，b满足|a|=2，|a+2b|=2，且(2a+b)⊥a，则|b|等于(　　)

A: 2 $\sqrt{3}$
B: 2 $\sqrt{2}$
C: 2
D: 1

解析:

因为|a|=2，|a+2b|=2，

所以(a+2b)²=a²+4a·b+4b²=4，

又(2a+b)⊥a，所以(2a+b)·a=0，

即2a²+b·a=0，

所以b·a=-2a²=-2×2²=-8，

则2²+4×(-8)+4|b|²=4，

解得|b|=2 $\sqrt{2}$ (负值舍去).

第5题 (单选题) 难度 - 基础题：

若平面向量a，b，c，两两夹角相等，且|a|=|b|=2，|c|=5，则|a+b+c|等于(　　)

A: $\sqrt{3}$
B: 9
C: 3或9
D: 3或 $\sqrt{3}$

解析:

因为平面上三个向量a，b，c，两两夹角相等，|a|=|b|=2，|c|=5，

当两两夹角为120°时，

|a+b+c|²=4+4+25+2×2×2×cos 120°+2×2×5×cos 120°+2×2×5×cos 120°=9，

所以|a+b+c|=3；

当两两夹角为0°时，|a+b+c|=2+2+5=9.

第6题 (单选题) 难度 - 基础题：

若O为△ABC所在平面内任一点，且满足( $\vec{O B}$ - $\vec{O C}$ )·( $\vec{O B}$ + $\vec{O C}$ -2 $\vec{O A}$ )=0，则△ABC的形状为(　　)

A: 等腰三角形
B: 直角三角形
C: 等边三角形
D: 等腰直角三角形

解析:

因为( $\vec{O B}$ - $\vec{O C}$ )·( $\vec{O B}$ + $\vec{O C}$ -2 $\vec{O A}$ )=0，

即 $\vec{C B}$ ·( $\vec{A B}$ + $\vec{A C}$ )=0，又因为 $\vec{A B}$ - $\vec{A C}$ = $\vec{C B}$ ，

所以( $\vec{A B}$ - $\vec{A C}$ )·( $\vec{A B}$ + $\vec{A C}$ )=0，

即| $\vec{A B}$ |=| $\vec{A C}$ |，所以△ABC是等腰三角形.

第7题 (多选题) 难度 - 基础题：

(多选)已知正三角形ABC的边长为2，设 $\vec{A B}$ =2a， $\vec{B C}$ =b，则下列结论正确的是(　　)

A: |a+b|=1
B: a⊥b
C: (4a+b)⊥b
D: a·b=-1

解析:

分析知|a|=1，|b|=2，a与b的夹角是120°，故B错误；

∵(a+b)²=|a|²+2a·b+|b|²

=1+2×1×2× $(- \frac{1}{2})$ +4=3，

∴|a+b|= $\sqrt{3}$ ，故A错误；

∵(4a+b)·b=4a·b+b²=4×1×2×cos 120°+4=0，∴(4a+b)⊥b，故C正确；

a·b=1×2×cos 120°=-1，故D正确.

第8题 (多选题) 难度 - 基础题：

(多选)已知向量a，b不共线且a·b=0，则下列结论一定正确的是(　　)

A: a=0或b=0
B: a⊥b
C: |a+b|=|a-b|
D: a，b在a+b上的投影向量相等

解析:

对于A，a，b不共线，A错误；

对于B，∵a·b=0，

∴a⊥b，B正确；

对于C，方法一　由向量加法和减法的几何意义，

|a+b|，|a-b|表示矩形的两条对角线长，是相等的，C正确；

方法二　由a·b=0，

则a²+2a·b+b²=a²-2a·b+b²，

则(a+b)²=(a-b)²，

则 $\sqrt{(a + b)^{2}}$ = $\sqrt{(a - b)^{2}}$ ，

则|a+b|=|a-b|，C正确；

对于D，根据矩形性质知a，b在a+b上的投影向量不一定相等，

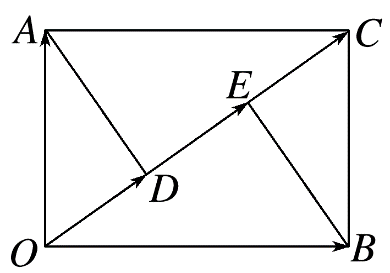
如图所示， $\vec{O A}$ =a， $\vec{O B}$ =b， $\vec{O C}$ =a+b，且a⊥b，a，b在a+b上的投影向量分别为 $\vec{O D}$ ， $\vec{O E}$ ，D错误.

第9题 (多选题) 难度 - 基础题：

(多选)已知向量a，b满足|a+2b|=|a|，|3a+b|=|a-b|，且|a|=2，则(　　)

A: |b|=2
B: a+b=0
C: |a-2b|=4
D: a·b=-4

解析:

由|a+2b|=|a|，得a²+4a·b+4b²=a²，

整理得a·b+b²=0.①

由|3a+b|=|a-b|，

得9a²+6a·b+b²=a²-2a·b+b²，

整理得a·b+a²=0.②

由①②及|a|=2，得a²=b²=4，

所以 $|b|$ =2，a·b=-4，故A，D正确；

cos〈a，b〉= $\frac{a \cdot b}{| a | | b |}$ = $\frac{- 4}{2 \times 2}$ =-1，所以〈a，b〉=π，所以a，b反向共线，

又|a|= $|b|$ =2，所以a+b=0，|a-2b|=3 $|a|$ =6，故B正确，C错误.

第10题 (填空题) 难度 - 基础题：

(课本P22练习T3改编)已知|a|=1，|b|=2，a与b的夹角为60°，则(a+b)²-(a-b)²=　　　　　　.

答案:

解析:

方法一　(a+b)²-(a-b)²

=(a+b+a-b)·(a+b-a+b)

=2a·2b=4a·b=4×1×2× $\frac{1}{2}$ =4.

方法二　(a+b)²-(a-b)²=(a²+2a·b+b²)-(a²-2a·b+b²)

=4a·b=4×1×2× $\frac{1}{2}$ =4.

第11题 (填空题) 难度 - 基础题：

已知e₁，e₂是互相垂直的单位向量，若 $\sqrt{3}$ e₁+e₂与e₁+λe₂的夹角为60°，则实数λ的值是　　　　.

答案:

- $\frac{\sqrt{3}}{3}$

解析:

因为| $\sqrt{3}$ e₁+e₂|= $\sqrt{(\sqrt{3} e_{1} + e_{2})^{2}}$ = $\sqrt{3 + 1}$ =2，|e₁+λe₂|= $\sqrt{(e_{1} + λ e_{2})^{2}}$ = $\sqrt{1 + λ^{2}}$ ，且 $(\sqrt{3} e_{1} + e_{2})$ · $(e_{1} + λ e_{2})$ = $\sqrt{3}$ +λ，

所以cos 60°= $\frac{\sqrt{3} + λ}{2 \cdot \sqrt{1 + λ^{2}}}$ = $\frac{1}{2}$ ，解得λ=- $\frac{\sqrt{3}}{3}$ .

第12题 (填空题) 难度 - 基础题：

在△ABC中，若 ${\vec{A B}}^{2}$ = $\vec{A B}$ · $\vec{A C}$ + $\vec{B A}$ · $\vec{B C}$ + $\vec{C A}$ · $\vec{C B}$ ，则△ABC的形状为　　　　　三角形.

答案:

直角

解析:

由 ${\vec{A B}}^{2}$ - $\vec{A B}$ · $\vec{A C}$ = $\vec{B A}$ · $\vec{B C}$ + $\vec{C A}$ · $\vec{C B}$ ，得 $\vec{A B}$ ·( $\vec{A B}$ - $\vec{A C}$ )= $\vec{B C}$ ·( $\vec{B A}$ - $\vec{C A}$ )，即 $\vec{A B}$ · $\vec{C B}$ = $\vec{B C}$ · $\vec{B C}$ ，

所以 $\vec{A B}$ · $\vec{B C}$ + $\vec{B C}$ · $\vec{B C}$ =0，即 $\vec{B C}$ ·( $\vec{A B}$ + $\vec{B C}$ )=0，则 $\vec{B C}$ · $\vec{A C}$ =0，即 $\vec{B C}$ ⊥ $\vec{A C}$ ，所以△ABC是直角三角形.

第13题 (填空题) 难度 - 基础题：

若两个非零向量a，b满足 $|a + b|$ = $|a - b|$ = $|2 a|$ ，则a-b与a的夹角为　　　　　.

答案:

$\frac{π}{3}$

解析:

设向量a-b与a的夹角为θ，因为|a+b|=|a-b|=|2a|=2|a|，

则 ${(a + b)}^{2}$ = ${(a - b)}^{2}$ =4a²，

变形得a²+b²+2a·b=a²+b²-2a·b=4a² ，

所以a·b=0 且b²=3a²，

则 $(a - b)$ ·a=a²= ${|a|}^{2}$ ，

故cos θ= $\frac{(a - b) \cdot a}{|a - b| |a|}$ = $\frac{{|a|}^{2}}{2 |a| \times |a|}$ = $\frac{1}{2}$ ，

又0≤θ≤π，则θ= $\frac{π}{3}$ .

第14题 (解答题) - 简答题难度 - 基础题：

(课本P23习题6.2T11)(1)已知|a|=3，|b|=4，且a与b的夹角θ=150°，求a·b，(a+b)²，|a+b|；

(2)已知|a|=2，|b|=5，且a·b=-3，求|a+b|，|a-b|.

答案:

解　(1)由|a|=3，|b|=4，且a与b的夹角θ=150°，

得a·b=|a||b|cos 150°

=3×4× $(- \frac{\sqrt{3}}{2})$ =-6 $\sqrt{3}$ ，

(a+b)²=|a|²+2a·b+|b|²=9+2×(-6 $\sqrt{3}$ )+16=25-12 $\sqrt{3}$ ，

|a+b|= $\sqrt{(a + b)^{2}}$ = $\sqrt{25 - 12 \sqrt{3}}$ .

(2)由|a|=2，|b|=5，且a·b=-3，

得|a+b|= $\sqrt{(a + b)^{2}}$ = $\sqrt{| a |^{2} + 2 a \cdot b + | b |^{2}}$

= $\sqrt{4 - 6 + 25}$ = $\sqrt{23}$ ，

|a-b|= $\sqrt{(a - b)^{2}}$ = $\sqrt{| a |^{2} - 2 a \cdot b + | b |^{2}}$

= $\sqrt{4 + 6 + 25}$ = $\sqrt{35}$ .

第15题 (解答题) - 简答题难度 - 基础题：

已知两个平面向量a与b的夹角为 $\frac{π}{3}$ ，且|a|=1，|b|=2，记m=3a-b，n=ta+2b.

(1)若m⊥n，求实数t的值；

(2)若t=2，m与n的夹角为θ，求cos θ.

答案:

解　(1)由m⊥n得m·n=0，

即m·n=(3a-b)·(ta+2b)

=3ta²+(6-t)a·b-2b²

=3t|a|²+(6-t)|a||b|cos $\frac{π}{3}$ -2|b|²

=3t+(6-t)×1×2× $\frac{1}{2}$ -2×2²=0，

解得t=1.

所以当m⊥n时，t=1.

(2)当t=2时，m=3a-b，n=2a+2b，

所以m·n=(3a-b)·(2a+2b)

=6a²+4a·b-2b²

=6|a|²+4|a||b|cos $\frac{π}{3}$ -2|b|²

=6+4×1×2× $\frac{1}{2}$ -2×2²=2，

|m|= $\sqrt{(3 a - b)^{2}}$ = $\sqrt{9 | a |^{2} - 6 a \cdot b + | b |^{2}}$ = $\sqrt{7}$ ，

|n|= $\sqrt{(2 a + 2 b)^{2}}$ = $\sqrt{4 | a |^{2} + 8 a \cdot b + 4 | b |^{2}}$

=2 $\sqrt{7}$ ，

所以cos θ= $\frac{m \cdot n}{| m | | n |}$ = $\frac{2}{\sqrt{7} \times 2 \sqrt{7}}$ = $\frac{1}{7}$ .

第16题 (解答题) - 简答题难度 - 基础题：

已知|a|=2，|b|=3，a与b的夹角为120°.

(1)求(2a-b)·(a+3b)与|a+b|的值；

(2)若xa-b与a+3b的夹角为钝角，求x的取值范围.

答案:

解　(1)因为|a|=2，|b|=3，a与b的夹角为120°，所以a·b=|a||b|cos 120°=2×3× $(- \frac{1}{2})$ =-3.

(2a-b)·(a+3b)=2a²+5a·b-3b²=2×4-15-3×9=-34.

|a+b|= $\sqrt{| a + b |^{2}}$ = $\sqrt{a^{2} + 2 a \cdot b + b^{2}}$

= $\sqrt{4 - 6 + 9}$ = $\sqrt{7}$ .

(2)因为xa-b与a+3b的夹角为钝角，

所以(xa-b)·(a+3b)=xa²+(3x-1)a·b-3b²=4x-9x+3-27<0，

即x>- $\frac{24}{5}$ .又当x=- $\frac{1}{3}$ 时，

xa-b与a+3b反向，

所以若xa-b与a+3b的夹角为钝角，x的取值范围是 $(- \frac{24}{5}, - \frac{1}{3})$ ∪ $(- \frac{1}{3}, + \infty)$ .

第17题 (填空题) 难度 - 基础题：

记△ABC的三个内角A，B，C的对边分别为a，b，c，且b=3，c=2，若O是△ABC的外心，则 $\vec{A O}$ · $\vec{B C}$ =　　　　　　 .

答案:

$\frac{5}{2}$

解析:

如图，作OD⊥AB于D，OE⊥AC于E，

∵在圆O中，OD⊥AB，

∴AD= $\frac{1}{2}$ AB，

因此 $\vec{A O}$ · $\vec{A B}$

= $|\vec{A D}| |\vec{A B}|$ = $\frac{1}{2} {|\vec{A B}|}^{2}$ =2，

同理可得 $\vec{A O}$ · $\vec{A C}$ = $\frac{1}{2} {|\vec{A C}|}^{2}$ = $\frac{9}{2}$ ，

∴ $\vec{A O}$ · $\vec{B C}$ = $\vec{A O}$ · $\vec{A C}$ - $\vec{A O}$ · $\vec{A B}$ = $\frac{9}{2}$ -2= $\frac{5}{2}$ .

第18题 (解答题) - 简答题难度 - 基础题：

已知同一平面内的三个向量a，b，c的模均为1，它们相互之间的夹角为120°.

(1)求证：(a-b)⊥c；

(2)若|ka+b+c|>1(k∈R)，求k的取值范围.

答案:

(1)证明　因为|a|=|b|=|c|=1，

且a，b，c之间的夹角均为120°，

所以(a-b)·c=a·c-b·c=|a||c|cos 120°-|b||c|cos 120°=0，

所以(a-b)⊥c.

(2)解　因为|ka+b+c|>1，

所以(ka+b+c)·(ka+b+c)>1，

即k²a²+b²+c²+2ka·b+2ka·c+2b·c>1.

因为a·b=a·c=b·c=cos 120°=- $\frac{1}{2}$ ，

所以k²-2k>0，解得k<0或k>2，

即k的取值范围是(-∞，0)∪(2，+∞).

第六章 作业6 向量的数量积(二)

第六章作业6 向量的数量积(二)